Kalau kamu ingin belajar geometri jarak titik ke garis secara lebih mendalam, coba simak penjelasan yang ada di sini. Setelah menerima materi, kamu bisa langsung mempraktikkannya dengan mengerjakan latihan soal yang telah kami sediakan.
Di sini, kamu akan belajar tentang Geometri Jarak Titik ke Garis melalui video yang dibawakan oleh Bapak Anton Wardaya. Kamu akan diajak untuk memahami materi hingga metode menyelesaikan soal.
Selain itu, kamu juga akan mendapatkan latihan soal interaktif dalam 3 tingkat kesulitan (mudah, sedang, sukar). Tentunya menarik, bukan? Penjelasan yang didapatkan bisa dipraktikkan secara langsung.
Sekarang, kamu bisa mulai belajar dengan 2 video dan 3 set latihan soal yang ada di halaman ini. Apabila materi ini berguna, bagikan ke teman atau rekan kamu supaya mereka juga mendapatkan manfaatnya.
Kamu dapat download modul & contoh soal serta kumpulan latihan soal lengkap dalam bentuk pdf pada list dibawah ini:
Contoh Soal Geometri Jarak Titik ke Garis (1)
Contoh Soal Geometri Jarak Titik ke Garis (2)
Latihan Soal Geometri Jarak Titik Ke Garis (Mudah)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
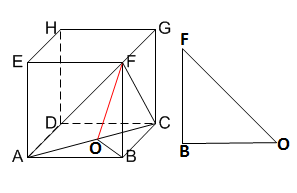
Diketahui kubus ABCD.EFGH dengan panjang rusuk 10 cm. Jarak titik F ke garis AC adalah…
BetulPerhatikan gambar berikut :

$AC=CF=AF=$ Diagonal Bidang $=10\sqrt{2}$
Perhatikan bahwa segitiga ACF adalah segitiga sama sisi.
Jika FO adalah jarak titik F ke garis AC, maka :
$\begin{aligned}FO & =\sqrt{AF^{2}-AO^{2}}\\
& =\sqrt{\left(10\sqrt{2}\right)^{2}-\left(5\sqrt{2}\right)^{2}}\\
& =\sqrt{200-50}\\
& =\sqrt{150}\\
& =5\sqrt{6}\, cm
\end{aligned}
$SalahPerhatikan gambar berikut :

$AC=CF=AF=$ Diagonal Bidang $=10\sqrt{2}$
Perhatikan bahwa segitiga ACF adalah segitiga sama sisi.
Jika FO adalah jarak titik F ke garis AC, maka :
$\begin{aligned}FO & =\sqrt{AF^{2}-AO^{2}}\\
& =\sqrt{\left(10\sqrt{2}\right)^{2}-\left(5\sqrt{2}\right)^{2}}\\
& =\sqrt{200-50}\\
& =\sqrt{150}\\
& =5\sqrt{6}\, cm
\end{aligned}
$ -
Pertanyaan ke 2 dari 5
2. Pertanyaan
Panjang rusuk pada kubus ABCD.EFGH adalah 6 cm. Jika titik Q berada pada AD sehingga AQ = 2. Jarak titik A ke garis BQ adalah…
BetulPerhatikan gambar berikut :

$\begin{aligned}BQ & =\sqrt{AQ^{2}+AB^{2}}\\
& =\sqrt{2^{2}+6^{2}}\\
& =\sqrt{4+36}\\
& =\sqrt{40}\\
& =2\sqrt{10}
\end{aligned}
$Perhatikan segitiga BAQ :
Luas segitiga BAQ adalah :
$\frac{1}{2}\cdot AB\cdot AQ=\frac{1}{2}\cdot BQ\cdot AA’$
$\begin{aligned}AA’ & =\frac{AB.AQ}{BQ}\\
& =\frac{6.2}{2\sqrt{10}}\\
& =\frac{6}{\sqrt{10}}.\frac{\sqrt{10}}{\sqrt{10}}\\
& =\frac{6}{10}\sqrt{10}\\
& =\frac{3}{5}\sqrt{10}
\end{aligned}
$SalahPerhatikan gambar berikut :

$\begin{aligned}BQ & =\sqrt{AQ^{2}+AB^{2}}\\
& =\sqrt{2^{2}+6^{2}}\\
& =\sqrt{4+36}\\
& =\sqrt{40}\\
& =2\sqrt{10}
\end{aligned}
$Perhatikan segitiga BAQ :
Luas segitiga BAQ adalah :
$\frac{1}{2}\cdot AB\cdot AQ=\frac{1}{2}\cdot BQ\cdot AA’$
$\begin{aligned}AA’ & =\frac{AB.AQ}{BQ}\\
& =\frac{6.2}{2\sqrt{10}}\\
& =\frac{6}{\sqrt{10}}.\frac{\sqrt{10}}{\sqrt{10}}\\
& =\frac{6}{10}\sqrt{10}\\
& =\frac{3}{5}\sqrt{10}
\end{aligned}
$ -
Pertanyaan ke 3 dari 5
3. Pertanyaan
Kubus ABCD.EFGH panjang rusuknya 4 cm. Titik P tengah tengah EH. Jarak titik P ke garis BG adalah…
BetulPerhatikan gambar berikut :


$\begin{aligned}AP & =PG\\
& =\sqrt{PH^{2}+HG^{2}}\\
& =\sqrt{2^{2}+4^{2}}\\
& =\sqrt{20}
\end{aligned}
$$BG=$Diagonal bidang $=4\sqrt{2}$
$\begin{aligned}BP & =\sqrt{AP^{2}+AB^{2}}\\
& =\sqrt{\left(\sqrt{20}\right)^{2}+4^{2}}\\
& =\sqrt{20+16}\\
& =6
\end{aligned}
$Perhatikan Segitiga BPG. Jika PO adalah jarak P ke garis BG maka :
$PO^{2}=PO^{2}$
$BP^{2}-BO^{2}=PG^{2}-GO^{2}$
$6^{2}-x^{2}=\left(\sqrt{20}\right)^{2}-\left(4\sqrt{2}-x\right)^{2}$
$36-x^{2}=20-\left(32-8\sqrt{2}x+x^{2}\right)$
$48=8\sqrt{2}x$
$x=\frac{48}{8\sqrt{2}}=\frac{6}{\sqrt{2}}$
$\Rightarrow x=\frac{6}{\sqrt{2}}.\frac{\sqrt{2}}{\sqrt{2}}=3\sqrt{2}$
$\begin{aligned}PO^{2} & =36-x^{2}\\
& =36-\left(3\sqrt{2}\right)^{2}\\
& =36-18\\
& =18
\end{aligned}
$$\begin{aligned}PO & =\sqrt{18}\\
& =3\sqrt{2}
\end{aligned}
$Jadi jarak titik P ke garis BG adalah $3\sqrt{2}.$
SalahPerhatikan gambar berikut :


$\begin{aligned}AP & =PG\\
& =\sqrt{PH^{2}+HG^{2}}\\
& =\sqrt{2^{2}+4^{2}}\\
& =\sqrt{20}
\end{aligned}
$$BG=$Diagonal bidang $=4\sqrt{2}$
$\begin{aligned}BP & =\sqrt{AP^{2}+AB^{2}}\\
& =\sqrt{\left(\sqrt{20}\right)^{2}+4^{2}}\\
& =\sqrt{20+16}\\
& =6
\end{aligned}
$Perhatikan Segitiga BPG. Jika PO adalah jarak P ke garis BG maka :
$PO^{2}=PO^{2}$
$BP^{2}-BO^{2}=PG^{2}-GO^{2}$
$6^{2}-x^{2}=\left(\sqrt{20}\right)^{2}-\left(4\sqrt{2}-x\right)^{2}$
$36-x^{2}=20-\left(32-8\sqrt{2}x+x^{2}\right)$
$48=8\sqrt{2}x$
$x=\frac{48}{8\sqrt{2}}=\frac{6}{\sqrt{2}}$
$\Rightarrow x=\frac{6}{\sqrt{2}}.\frac{\sqrt{2}}{\sqrt{2}}=3\sqrt{2}$
$\begin{aligned}PO^{2} & =36-x^{2}\\
& =36-\left(3\sqrt{2}\right)^{2}\\
& =36-18\\
& =18
\end{aligned}
$$\begin{aligned}PO & =\sqrt{18}\\
& =3\sqrt{2}
\end{aligned}
$Jadi jarak titik P ke garis BG adalah $3\sqrt{2}.$
-
Pertanyaan ke 4 dari 5
4. Pertanyaan
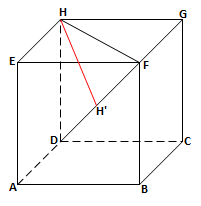
Pada kubus ABCD.EFGH, jarak titik H ke DF adalah…
BetulPerhatikan gambar berikut :

Misalkan panjang rusuk kubus adalah a cm
HF (Diagonal Bidang) = a$\sqrt{2}$cm
DF (Diagonal Ruang) = a$\sqrt{3}$ cm
Misalkan HH’ adalah jarak dari titik H ke DF
Perhatikan segitiga DHF yang siku-siku di H.
Luas segitiga DHF.
$\frac{1}{2}\cdot DH\cdot HF=\frac{1}{2}\cdot DF\cdot HH’$
$\begin{aligned}HH’ & =\frac{DH\cdot HF}{DF}\\
& =\frac{a\cdot a\sqrt{2}}{a\sqrt{3}}\\
& =\frac{1}{3}a\sqrt{6}
\end{aligned}
$SalahPerhatikan gambar berikut :

Misalkan panjang rusuk kubus adalah a cm
HF (Diagonal Bidang) = a$\sqrt{2}$cm
DF (Diagonal Ruang) = a$\sqrt{3}$ cm
Misalkan HH’ adalah jarak dari titik H ke DF
Perhatikan segitiga DHF yang siku-siku di H.
Luas segitiga DHF.
$\frac{1}{2}\cdot DH\cdot HF=\frac{1}{2}\cdot DF\cdot HH’$
$\begin{aligned}HH’ & =\frac{DH\cdot HF}{DF}\\
& =\frac{a\cdot a\sqrt{2}}{a\sqrt{3}}\\
& =\frac{1}{3}a\sqrt{6}
\end{aligned}
$ -
Pertanyaan ke 5 dari 5
5. Pertanyaan
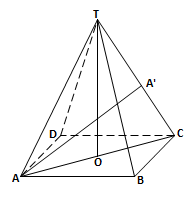
Diketahui limas beraturan T.ABCD. panjang rusuk alas 8 cm dan panjang rusuk tegaknya adalah 8$\sqrt{2}$cm. Jarak A ke garis TC adalah…
BetulPerhatikan gambar berikut :

Perhatikan segitiga TAC.
$\begin{aligned}AB & =BC\\
& =CD\\
& =AD\\
& =8\, cm
\end{aligned}
$$\begin{aligned}TA & =TB\\
& =TC\\
& =TD\\
& =8\sqrt{2}
\end{aligned}
$AC adalah diagonal bidang. AC = 8$\sqrt{2}$ cm
$\begin{aligned}AO & =OC\\
& =4\sqrt{2}\, cm
\end{aligned}
$$\begin{aligned}TO & =\sqrt{AT^{2}-AO^{2}}\\
& =\sqrt{\left(8\sqrt{2}\right)^{2}-\left(4\sqrt{2}\right)^{2}}\\
& =\sqrt{128-32}\\
& =\sqrt{96}\\
& =4\sqrt{6}
\end{aligned}
$Misalkan AA’ adalah jarak dari A ke garis TC.
Perhatikan segitiga TAC :
Luas segitiga TAC :
$\frac{1}{2}\cdot AC\cdot TO=\frac{1}{2}\cdot TC\cdot AA’$
$\begin{aligned}AA’ & =\frac{AC.TO}{TC}\\
& =\frac{8\sqrt{2}\cdot4\sqrt{6}}{8\sqrt{2}}\\
& =4\sqrt{6}
\end{aligned}
$SalahPerhatikan gambar berikut :

Perhatikan segitiga TAC.
$\begin{aligned}AB & =BC\\
& =CD\\
& =AD\\
& =8\, cm
\end{aligned}
$$\begin{aligned}TA & =TB\\
& =TC\\
& =TD\\
& =8\sqrt{2}
\end{aligned}
$AC adalah diagonal bidang. AC = 8$\sqrt{2}$ cm
$\begin{aligned}AO & =OC\\
& =4\sqrt{2}\, cm
\end{aligned}
$$\begin{aligned}TO & =\sqrt{AT^{2}-AO^{2}}\\
& =\sqrt{\left(8\sqrt{2}\right)^{2}-\left(4\sqrt{2}\right)^{2}}\\
& =\sqrt{128-32}\\
& =\sqrt{96}\\
& =4\sqrt{6}
\end{aligned}
$Misalkan AA’ adalah jarak dari A ke garis TC.
Perhatikan segitiga TAC :
Luas segitiga TAC :
$\frac{1}{2}\cdot AC\cdot TO=\frac{1}{2}\cdot TC\cdot AA’$
$\begin{aligned}AA’ & =\frac{AC.TO}{TC}\\
& =\frac{8\sqrt{2}\cdot4\sqrt{6}}{8\sqrt{2}}\\
& =4\sqrt{6}
\end{aligned}
$
Latihan Soal Geometri Jarak Titik Ke Garis (Sedang)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Kubus $ABCD.EFGH$ panjang rusuknya $4$ cm. Titik P tengah tengah EH. Jarak titik P ke garis BG adalah…
BetulPerhatikan gambar berikut :


$\begin{aligned}PG & =\sqrt{PH^{2}+HG^{2}}\\
& =\sqrt{2^{2}+4^{2}}\\
& =\sqrt{20}
\end{aligned}
$$BG=$Diagonal bidang $=4\sqrt{2}$
$\begin{aligned}BP & =\sqrt{AP^{2}+AB^{2}}\\
& =\sqrt{\left(\sqrt{20}\right)^{2}+4^{2}}\\
& =\sqrt{20+16}\\
& =6
\end{aligned}
$Perhatikan Segitiga BPG. Jika PO adalah jarak P ke garis BG maka :
$PO^{2}=PO^{2}$
$BP^{2}-BO^{2}=PG^{2}-GO^{2}$
$6^{2}-x^{2}=\left(\sqrt{20}\right)^{2}-\left(4\sqrt{2}-x\right)^{2}$
$36-x^{2}=20-\left(32-8\sqrt{2}x+x^{2}\right)$
$\begin{aligned}48 & =8\sqrt{2}x\\
\Rightarrow x & =\frac{6}{\sqrt{2}}\cdot\frac{\sqrt{2}}{\sqrt{2}}\\
& =3\sqrt{2}
\end{aligned}
$$\begin{aligned}PO^{2} & =36-x^{2}\\
& =36-\left(3\sqrt{2}\right)^{2}\\
& =36-18\\
& =18
\end{aligned}
$$\begin{aligned}PO & =\sqrt{18}\\
& =3\sqrt{2}
\end{aligned}
$Jadi jarak titik P ke garis BG adalah $3\sqrt{2}.$
SalahPerhatikan gambar berikut :


$\begin{aligned}PG & =\sqrt{PH^{2}+HG^{2}}\\
& =\sqrt{2^{2}+4^{2}}\\
& =\sqrt{20}
\end{aligned}
$$BG=$Diagonal bidang $=4\sqrt{2}$
$\begin{aligned}BP & =\sqrt{AP^{2}+AB^{2}}\\
& =\sqrt{\left(\sqrt{20}\right)^{2}+4^{2}}\\
& =\sqrt{20+16}\\
& =6
\end{aligned}
$Perhatikan Segitiga BPG. Jika PO adalah jarak P ke garis BG maka :
$PO^{2}=PO^{2}$
$BP^{2}-BO^{2}=PG^{2}-GO^{2}$
$6^{2}-x^{2}=\left(\sqrt{20}\right)^{2}-\left(4\sqrt{2}-x\right)^{2}$
$36-x^{2}=20-\left(32-8\sqrt{2}x+x^{2}\right)$
$\begin{aligned}48 & =8\sqrt{2}x\\
\Rightarrow x & =\frac{6}{\sqrt{2}}\cdot\frac{\sqrt{2}}{\sqrt{2}}\\
& =3\sqrt{2}
\end{aligned}
$$\begin{aligned}PO^{2} & =36-x^{2}\\
& =36-\left(3\sqrt{2}\right)^{2}\\
& =36-18\\
& =18
\end{aligned}
$$\begin{aligned}PO & =\sqrt{18}\\
& =3\sqrt{2}
\end{aligned}
$Jadi jarak titik P ke garis BG adalah $3\sqrt{2}.$
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Pada kubus ABCD.EFGH, jarak titik H ke DF adalah…
BetulPerhatikan gambar berikut :

Misalkan panjang rusuk kubus adalah a cm
HF (Diagonal Bidang) $=a\sqrt{2}$ cm
DF (Diagonal Ruang) $=a\sqrt{3}$ cm
Misalkan HH’ adalah jarak dari titik H ke DF
Perhatikan segitiga DHF yang siku-siku di H.
Luas segitiga DHF.
$\frac{1}{2}\cdot DH\cdot HF=\frac{1}{2}\cdot DF\cdot HH’$
$\begin{aligned}HH’ & =\frac{DH\cdot HF}{DF}\\
& =\frac{a\cdot a\sqrt{2}}{a\sqrt{3}}\\
& =\frac{1}{3}a\sqrt{6}
\end{aligned}
$SalahPerhatikan gambar berikut :

Misalkan panjang rusuk kubus adalah a cm
HF (Diagonal Bidang) $=a\sqrt{2}$ cm
DF (Diagonal Ruang) $=a\sqrt{3}$ cm
Misalkan HH’ adalah jarak dari titik H ke DF
Perhatikan segitiga DHF yang siku-siku di H.
Luas segitiga DHF.
$\frac{1}{2}\cdot DH\cdot HF=\frac{1}{2}\cdot DF\cdot HH’$
$\begin{aligned}HH’ & =\frac{DH\cdot HF}{DF}\\
& =\frac{a\cdot a\sqrt{2}}{a\sqrt{3}}\\
& =\frac{1}{3}a\sqrt{6}
\end{aligned}
$ -
Pertanyaan ke 3 dari 5
3. Pertanyaan
Diketahui limas beraturan T.ABCD. panjang rusuk alas $8$ cm dan panjang rusuk tegaknya adalah $8\sqrt{2}$cm. Jarak A ke garis TC adalah…
BetulPerhatikan gambar berikut :

Perhatikan segitiga TAC.
$\begin{aligned}AB & =BC\\
& =CD\\
& =AD\\
& =8\, cm
\end{aligned}
$$\begin{aligned}TA & =TB\\
& =TC\\
& =TD\\
& =8\sqrt{2}
\end{aligned}
$AC adalah diagonal bidang. AC $=8\sqrt{2}$ cm
$\begin{aligned}AO & =OC\\
& =4\sqrt{2}\, cm
\end{aligned}
$$\begin{aligned}TO & =\sqrt{AT^{2}-AO^{2}}\\
& =\sqrt{\left(8\sqrt{2}\right)^{2}-\left(4\sqrt{2}\right)^{2}}\\
& =\sqrt{128-32}\\
& =\sqrt{96}\\
& =4\sqrt{6}
\end{aligned}
$Misalkan AA’ adalah jarak dari A ke garis TC.
Perhatikan segitiga TAC :
Luas segitiga TAC :
$\frac{1}{2}\cdot AC\cdot TO=\frac{1}{2}\cdot TC\cdot AA’$
$\begin{aligned}AA’ & =\frac{AC\cdot TO}{TC}\\
& =\frac{8\sqrt{2}\cdot4\sqrt{6}}{8\sqrt{2}}\\
& =4\sqrt{6}
\end{aligned}
$SalahPerhatikan gambar berikut :

Perhatikan segitiga TAC.
$\begin{aligned}AB & =BC\\
& =CD\\
& =AD\\
& =8\, cm
\end{aligned}
$$\begin{aligned}TA & =TB\\
& =TC\\
& =TD\\
& =8\sqrt{2}
\end{aligned}
$AC adalah diagonal bidang. AC $=8\sqrt{2}$ cm
$\begin{aligned}AO & =OC\\
& =4\sqrt{2}\, cm
\end{aligned}
$$\begin{aligned}TO & =\sqrt{AT^{2}-AO^{2}}\\
& =\sqrt{\left(8\sqrt{2}\right)^{2}-\left(4\sqrt{2}\right)^{2}}\\
& =\sqrt{128-32}\\
& =\sqrt{96}\\
& =4\sqrt{6}
\end{aligned}
$Misalkan AA’ adalah jarak dari A ke garis TC.
Perhatikan segitiga TAC :
Luas segitiga TAC :
$\frac{1}{2}\cdot AC\cdot TO=\frac{1}{2}\cdot TC\cdot AA’$
$\begin{aligned}AA’ & =\frac{AC\cdot TO}{TC}\\
& =\frac{8\sqrt{2}\cdot4\sqrt{6}}{8\sqrt{2}}\\
& =4\sqrt{6}
\end{aligned}
$ -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Diketahui kubus ABCD.EFGH dengan panjang rusuk a. Jika titik P terletak pada perpanjangan AB sehingga PB = 2a dan titik Q pada perpanjangan FG sehingga QG = a, panjang PQ adalah…
BetulPerhatikan gambar berikut :

PB tegak lurus bidang BCGF, BQ tegak lurus PB
$\begin{aligned}BQ & =\sqrt{FB^{2}+FQ^{2}}\\
& =\sqrt{a^{2}+\left(2a\right)^{2}}\\
& =\sqrt{5a^{2}}\\
& =a\sqrt{5}
\end{aligned}
$$\begin{aligned}PQ & =\sqrt{BQ^{2}+PB^{2}}\\
& =\sqrt{\left(a\sqrt{5}\right)^{2}+\left(2a\right)^{2}}\\
& =\sqrt{5a^{2}+4a^{2}}\\
& =\sqrt{9a^{2}}\\
& =3a
\end{aligned}
$SalahPerhatikan gambar berikut :

PB tegak lurus bidang BCGF, BQ tegak lurus PB
$\begin{aligned}BQ & =\sqrt{FB^{2}+FQ^{2}}\\
& =\sqrt{a^{2}+\left(2a\right)^{2}}\\
& =\sqrt{5a^{2}}\\
& =a\sqrt{5}
\end{aligned}
$$\begin{aligned}PQ & =\sqrt{BQ^{2}+PB^{2}}\\
& =\sqrt{\left(a\sqrt{5}\right)^{2}+\left(2a\right)^{2}}\\
& =\sqrt{5a^{2}+4a^{2}}\\
& =\sqrt{9a^{2}}\\
& =3a
\end{aligned}
$ -
Pertanyaan ke 5 dari 5
5. Pertanyaan
Diketahui kubus ABCD.EFGH memiliki volume 1 liter. Jarak titik F ke garis AC adalah…cm
Betul$V=s^{3}=1l$
$1l=1000\, cm^{3}$
$\Rightarrow s=10\, cm$
Perhatikan gambar berikut :

Perhatikan bahwa AC = AF = CF = Diagonal ruang $=10\sqrt{2}$ cm
Dengan demikian segitiga ACF sama sisi. Oleh karena itu garis FO tegak lurus terhadap garis AC
$\begin{aligned}BO & =\frac{1}{2}BD\\
& =5\sqrt{2}\, cm
\end{aligned}
$FO adalah jarak F ke garis AC. Perhatikan segitiga FBO
$\begin{aligned}FO & =\sqrt{FB^{^{2}}+OB^{2}}\\
& =\sqrt{\left(10\right)^{2}+\left(5\sqrt{2}\right)^{2}}\\
& =\sqrt{100+50}\\
& =\sqrt{150}\\
& =5\sqrt{6}\, cm
\end{aligned}
$Salah$V=s^{3}=1l$
$1l=1000\, cm^{3}$
$\Rightarrow s=10\, cm$
Perhatikan gambar berikut :

Perhatikan bahwa AC = AF = CF = Diagonal ruang $=10\sqrt{2}$ cm
Dengan demikian segitiga ACF sama sisi. Oleh karena itu garis FO tegak lurus terhadap garis AC
$\begin{aligned}BO & =\frac{1}{2}BD\\
& =5\sqrt{2}\, cm
\end{aligned}
$FO adalah jarak F ke garis AC. Perhatikan segitiga FBO
$\begin{aligned}FO & =\sqrt{FB^{^{2}}+OB^{2}}\\
& =\sqrt{\left(10\right)^{2}+\left(5\sqrt{2}\right)^{2}}\\
& =\sqrt{100+50}\\
& =\sqrt{150}\\
& =5\sqrt{6}\, cm
\end{aligned}
$
Latihan Soal Geometri Jarak Titik Ke Garis (Sukar)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
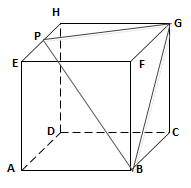
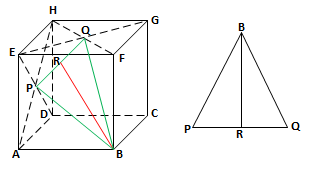
Diketahui panjang rusuk kubus ABCD.EFGH adalah 2a. Jika P titik tengah BF dan Q titik tengah EH, maka panjang PR adalah…
BetulPerhatikan gambar berikut :

$\begin{aligned}QE & =ER\\
& =a
\end{aligned}
$$\begin{aligned}QR & =\sqrt{QE^{2}+ER^{2}}\\
& =\sqrt{a^{2}+a^{2}}\\
& =a\sqrt{2}
\end{aligned}
$Perhatikan segitiga PQR , siku siku di Q :
$\begin{aligned}PR & =\sqrt{PQ^{2}+QR^{2}}\\
& =\sqrt{a^{2}+\left(a\sqrt{2}\right)^{2}}\\
& =\sqrt{3a^{2}}\\
& =a\sqrt{3}
\end{aligned}
$SalahPerhatikan gambar berikut :

$\begin{aligned}QE & =ER\\
& =a
\end{aligned}
$$\begin{aligned}QR & =\sqrt{QE^{2}+ER^{2}}\\
& =\sqrt{a^{2}+a^{2}}\\
& =a\sqrt{2}
\end{aligned}
$Perhatikan segitiga PQR , siku siku di Q :
$\begin{aligned}PR & =\sqrt{PQ^{2}+QR^{2}}\\
& =\sqrt{a^{2}+\left(a\sqrt{2}\right)^{2}}\\
& =\sqrt{3a^{2}}\\
& =a\sqrt{3}
\end{aligned}
$ -
Pertanyaan ke 2 dari 5
2. Pertanyaan
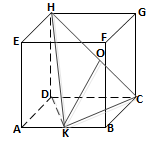
Diketahui kubus ABCD.EFGH. Titik K adalah perpotongan antara garis EG dan FH. Jarak dari titik K ke garis BG adalah…
BetulPerhatikan gambar berikut :

Perhatikan segitiga BKG tegak lurus di K.
Misalkan Jarak titik K ke garis BG adalah KI
Misalkan panjang rusuk adalah 4 cm
$\begin{aligned}EK & =KG\\
& =\frac{1}{2}EG\\
& =\frac{4}{2}\sqrt{2}\\
& =2\sqrt{2}\, cm
\end{aligned}
$$\begin{aligned}BK & =\sqrt{BF^{2}+FK^{2}}\\
& =\sqrt{4^{2}+\left(2\sqrt{2}\right)^{2}}\\
& =\sqrt{16+8}\\
& =2\sqrt{6}
\end{aligned}
$Perhatikan segitiga BKG luasnya adalah :
$\frac{1}{2}\cdot BK\cdot KG=\frac{1}{2}\cdot BG\cdot KI$
$\begin{aligned}KI & =\frac{BK.KG}{BG}\\
& =\frac{\left(2\sqrt{6}\right)\left(2\sqrt{2}\right)}{4\sqrt{2}}\\
& =\sqrt{6}
\end{aligned}
$Jadi jarak dari titik K ke garis BG adalah $\sqrt{6}$ cm
SalahPerhatikan gambar berikut :

Perhatikan segitiga BKG tegak lurus di K.
Misalkan Jarak titik K ke garis BG adalah KI
Misalkan panjang rusuk adalah 4 cm
$\begin{aligned}EK & =KG\\
& =\frac{1}{2}EG\\
& =\frac{4}{2}\sqrt{2}\\
& =2\sqrt{2}\, cm
\end{aligned}
$$\begin{aligned}BK & =\sqrt{BF^{2}+FK^{2}}\\
& =\sqrt{4^{2}+\left(2\sqrt{2}\right)^{2}}\\
& =\sqrt{16+8}\\
& =2\sqrt{6}
\end{aligned}
$Perhatikan segitiga BKG luasnya adalah :
$\frac{1}{2}\cdot BK\cdot KG=\frac{1}{2}\cdot BG\cdot KI$
$\begin{aligned}KI & =\frac{BK.KG}{BG}\\
& =\frac{\left(2\sqrt{6}\right)\left(2\sqrt{2}\right)}{4\sqrt{2}}\\
& =\sqrt{6}
\end{aligned}
$Jadi jarak dari titik K ke garis BG adalah $\sqrt{6}$ cm
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Titik P adalah titik potong antara garis AH dan DE dan titik P perpotongan antara garis EG dan FH. Jarak titik B ke garis PQ adalah….cm
BetulPerhatikan gambar berikut :

Perhatikan segitiga PBQ adalah segitiga sama kaki dimana PB = QB
Misalkan jarak dari titik B ke garis PQ adalah BR
$\begin{aligned}PR & =RQ\\
& =\frac{1}{2}PQ
\end{aligned}
$$\begin{aligned}PB & =\sqrt{AB^{2}+AP^{2}}\\
& =\sqrt{4^{2}+\left(2\sqrt{2}\right)^{2}}\\
& =\sqrt{16+8}\\
& =\sqrt{24}\\
& =2\sqrt{6}\, cm
\end{aligned}
$$\begin{aligned}PQ & =\sqrt{PH^{2}+HQ^{2}}\\
& =\sqrt{\left(2\sqrt{2}\right)^{2}+\left(2\sqrt{2}\right)^{2}}\\
& =\sqrt{8+8}\\
& =\sqrt{16}\\
& =4\, cm
\end{aligned}
$$\begin{aligned}PR & =RQ\\
& =\frac{1}{2}PQ\\
& =2
\end{aligned}
$$\begin{aligned}BR & =\sqrt{PB^{2}+PR^{2}}\\
& =\sqrt{\left(2\sqrt{6}\right)^{2}-2^{2}}\\
& =\sqrt{24-4}\\
& =\sqrt{20}\\
& =2\sqrt{5}\, cm
\end{aligned}
$Jadi jarak titik B ke garis PQ adalah $2\sqrt{5}$ cm
SalahPerhatikan gambar berikut :

Perhatikan segitiga PBQ adalah segitiga sama kaki dimana PB = QB
Misalkan jarak dari titik B ke garis PQ adalah BR
$\begin{aligned}PR & =RQ\\
& =\frac{1}{2}PQ
\end{aligned}
$$\begin{aligned}PB & =\sqrt{AB^{2}+AP^{2}}\\
& =\sqrt{4^{2}+\left(2\sqrt{2}\right)^{2}}\\
& =\sqrt{16+8}\\
& =\sqrt{24}\\
& =2\sqrt{6}\, cm
\end{aligned}
$$\begin{aligned}PQ & =\sqrt{PH^{2}+HQ^{2}}\\
& =\sqrt{\left(2\sqrt{2}\right)^{2}+\left(2\sqrt{2}\right)^{2}}\\
& =\sqrt{8+8}\\
& =\sqrt{16}\\
& =4\, cm
\end{aligned}
$$\begin{aligned}PR & =RQ\\
& =\frac{1}{2}PQ\\
& =2
\end{aligned}
$$\begin{aligned}BR & =\sqrt{PB^{2}+PR^{2}}\\
& =\sqrt{\left(2\sqrt{6}\right)^{2}-2^{2}}\\
& =\sqrt{24-4}\\
& =\sqrt{20}\\
& =2\sqrt{5}\, cm
\end{aligned}
$Jadi jarak titik B ke garis PQ adalah $2\sqrt{5}$ cm
-
Pertanyaan ke 4 dari 5
4. Pertanyaan
Diketahui kubus ABCD.EFGH dengan panjang rusuk $12$ cm. K adalah titik tengah rusuk AB. Jarak titik K ke garis HC adalah ….cm
BetulPerhatikan gambar berikut :

$CH$ (Diagonal Bidang) $=12\sqrt{2}$ cm
$\begin{aligned}CK & =\sqrt{BK^{2}+BC^{2}}\\
& =\sqrt{6^{2}+12^{2}}\\
& =\sqrt{36+144}\\
& =\sqrt{180}\\
& =6\sqrt{5}\, cm
\end{aligned}
$$KD=CK$
$\begin{aligned}KH & =\sqrt{DH^{2}+KD^{2}}\\
& =\sqrt{12^{2}+\left(6\sqrt{5}\right)^{2}}\\
& =\sqrt{144+180}\\
& =\sqrt{324}\\
& =18\, cm
\end{aligned}
$Perhatikan segitiga KCH
$\begin{aligned}\cos\angle KCH & =\frac{CK^{2}+CH^{2}-KH^{2}}{2\cdot CH\cdot KH}\\
& =\frac{\left(6\sqrt{5}\right)^{2}+\left(12\sqrt{2}\right)^{2}-18^{2}}{2\cdot6\sqrt{5}\cdot12\sqrt{2}}\\
& =\frac{180+288-324}{144\sqrt{10}}\\
& =\frac{144}{144\sqrt{10}}\\
& =\frac{1}{\sqrt{10}}
\end{aligned}
$KO adalah jarak dari K ke garis CH
$\sin\angle KCH=\frac{3}{\sqrt{10}}$
$\frac{KO}{CK}=\frac{3}{\sqrt{10}}$
$\begin{aligned}KO & =CK\cdot\frac{3}{\sqrt{10}}\\
& =6\sqrt{5}\cdot\frac{3}{\sqrt{10}}\\
& =\frac{18}{\sqrt{2}}\cdot\frac{\sqrt{2}}{\sqrt{2}}\\
& =9\sqrt{2}
\end{aligned}
$SalahPerhatikan gambar berikut :

$CH$ (Diagonal Bidang) $=12\sqrt{2}$ cm
$\begin{aligned}CK & =\sqrt{BK^{2}+BC^{2}}\\
& =\sqrt{6^{2}+12^{2}}\\
& =\sqrt{36+144}\\
& =\sqrt{180}\\
& =6\sqrt{5}\, cm
\end{aligned}
$$KD=CK$
$\begin{aligned}KH & =\sqrt{DH^{2}+KD^{2}}\\
& =\sqrt{12^{2}+\left(6\sqrt{5}\right)^{2}}\\
& =\sqrt{144+180}\\
& =\sqrt{324}\\
& =18\, cm
\end{aligned}
$Perhatikan segitiga KCH
$\begin{aligned}\cos\angle KCH & =\frac{CK^{2}+CH^{2}-KH^{2}}{2\cdot CH\cdot KH}\\
& =\frac{\left(6\sqrt{5}\right)^{2}+\left(12\sqrt{2}\right)^{2}-18^{2}}{2\cdot6\sqrt{5}\cdot12\sqrt{2}}\\
& =\frac{180+288-324}{144\sqrt{10}}\\
& =\frac{144}{144\sqrt{10}}\\
& =\frac{1}{\sqrt{10}}
\end{aligned}
$KO adalah jarak dari K ke garis CH
$\sin\angle KCH=\frac{3}{\sqrt{10}}$
$\frac{KO}{CK}=\frac{3}{\sqrt{10}}$
$\begin{aligned}KO & =CK\cdot\frac{3}{\sqrt{10}}\\
& =6\sqrt{5}\cdot\frac{3}{\sqrt{10}}\\
& =\frac{18}{\sqrt{2}}\cdot\frac{\sqrt{2}}{\sqrt{2}}\\
& =9\sqrt{2}
\end{aligned}
$ -
Pertanyaan ke 5 dari 5
5. Pertanyaan
Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm dan T adalah titik tengah CG. Jarak titik E ke BT adalah…
BetulPerhatikan gambar berikut :

Misalkan jarak dari E ke garis BT adalah EE’
$BE$(Diagonal Bidang) $=6\sqrt{2}$ cm
$\begin{aligned}BT & =\sqrt{BC^{2}+CT^{2}}\\
& =\sqrt{6^{2}+3^{2}}\\
& =\sqrt{36+9}\\
& =\sqrt{45}\\
& =3\sqrt{5}\, cm
\end{aligned}
$$\begin{aligned}BT & =FT\\
& =3\sqrt{5}\, cm
\end{aligned}
$$\begin{aligned}ET & =\sqrt{EF^{2}+FT^{2}}\\
& =\sqrt{6^{2}+\left(3\sqrt{5}\right)^{2}}\\
& =\sqrt{36+45}\\
& =\sqrt{81}\\
& =9
\end{aligned}
$Perhatikan segitiga BET
$\begin{aligned}\cos\alpha & =\frac{BT^{2}+ET^{2}-BE^{2}}{2\cdot BT\cdot ET}\\
& =\frac{\left(3\sqrt{5}\right)^{2}+9^{2}-\left(6\sqrt{2}\right)^{2}}{2\cdot3\sqrt{5}\cdot9}\\
& =\frac{45+81-72}{54\sqrt{5}}\\
& =\frac{54}{54\sqrt{5}}\\
& =\frac{1}{\sqrt{5}}
\end{aligned}
$sin$\alpha=\frac{2}{\sqrt{5}}$…(1)
Perhatikan segitiga BET
sin$\alpha=\frac{EE’}{ET}=\frac{EE’}{9}$…(2)
substitusikan pers (1) ke pers (2) sehingga :
$\frac{2}{\sqrt{5}}=\frac{EE’}{9}$
$\begin{aligned}EE’ & =\frac{18}{\sqrt{5}}\cdot\frac{\sqrt{5}}{\sqrt{5}}\\
& =\frac{18}{5}\sqrt{5}
\end{aligned}
$Jadi jarak dari E ke garis BT adalah $\frac{18}{5}\sqrt{5}$.
SalahPerhatikan gambar berikut :

Misalkan jarak dari E ke garis BT adalah EE’
$BE$(Diagonal Bidang) $=6\sqrt{2}$ cm
$\begin{aligned}BT & =\sqrt{BC^{2}+CT^{2}}\\
& =\sqrt{6^{2}+3^{2}}\\
& =\sqrt{36+9}\\
& =\sqrt{45}\\
& =3\sqrt{5}\, cm
\end{aligned}
$$\begin{aligned}BT & =FT\\
& =3\sqrt{5}\, cm
\end{aligned}
$$\begin{aligned}ET & =\sqrt{EF^{2}+FT^{2}}\\
& =\sqrt{6^{2}+\left(3\sqrt{5}\right)^{2}}\\
& =\sqrt{36+45}\\
& =\sqrt{81}\\
& =9
\end{aligned}
$Perhatikan segitiga BET
$\begin{aligned}\cos\alpha & =\frac{BT^{2}+ET^{2}-BE^{2}}{2\cdot BT\cdot ET}\\
& =\frac{\left(3\sqrt{5}\right)^{2}+9^{2}-\left(6\sqrt{2}\right)^{2}}{2\cdot3\sqrt{5}\cdot9}\\
& =\frac{45+81-72}{54\sqrt{5}}\\
& =\frac{54}{54\sqrt{5}}\\
& =\frac{1}{\sqrt{5}}
\end{aligned}
$sin$\alpha=\frac{2}{\sqrt{5}}$…(1)
Perhatikan segitiga BET
sin$\alpha=\frac{EE’}{ET}=\frac{EE’}{9}$…(2)
substitusikan pers (1) ke pers (2) sehingga :
$\frac{2}{\sqrt{5}}=\frac{EE’}{9}$
$\begin{aligned}EE’ & =\frac{18}{\sqrt{5}}\cdot\frac{\sqrt{5}}{\sqrt{5}}\\
& =\frac{18}{5}\sqrt{5}
\end{aligned}
$Jadi jarak dari E ke garis BT adalah $\frac{18}{5}\sqrt{5}$.