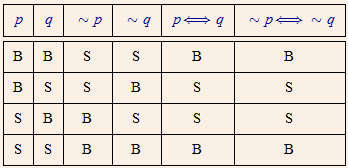
Tak jarang soal Matematika, khususnya biimplikasi cukup membingungkan untuk diselesaikan. Kalau kamu juga merasa demikian, artinya kamu masih perlu belajar lagi. Yuk, pelajari materi biimplikasi lewat uraian berikut!
Lewat artikel ini, kamu akan belajar tentang Biimplikasi melalui video yang dibawakan oleh Bapak Anton Wardaya. Kamu akan diajak untuk memahami materi hingga metode menyelesaikan soal.
Setelahnya, kamu juga akan mendapatkan latihan soal interaktif dalam 3 tingkat kesulitan (mudah, sedang, sukar). Oleh karenanya, pembahasan ini bisa langsung kamu praktikkan.
Sekarang, kamu bisa mulai belajar dengan 2 video dan 3 set latihan soal yang ada di halaman ini. Apabila materi ini berguna, bagikan ke teman atau rekan kamu supaya mereka juga mendapatkan manfaatnya.
Kamu dapat download modul & contoh soal serta kumpulan latihan soal lengkap dalam bentuk pdf pada list dibawah ini:
Pengertian Biimplikasi
Biimplikasi & Negasinya
Latihan Soal Biimplikasi (Mudah)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Diketahui pernyataan berikut ini:
$p :$ Eka rajin belajar
$q :$ Eka lulus Ujian Nasioanal
pernyataan majemuk dari dua pernyataan di atas yang diwakili oleh lambang $p\Longleftrightarrow\sim q$ adalah….Betulpernyataan untuk biimplikasi “jika dan hanya jika yang disimbolkan
dengan “$\Longleftrightarrow$”
$p\Longleftrightarrow q$ dibaca p jika dan hanya jika q
Jadi pernyataan$p\Longleftrightarrow\sim q$ dapat dinyatakan “Eka rajin belajar jika dan hanya jika ia tidak lulus ujian nasional “Salahpernyataan untuk biimplikasi “jika dan hanya jika yang disimbolkan
dengan “$\Longleftrightarrow$”
$p\Longleftrightarrow q$ dibaca p jika dan hanya jika q
Jadi pernyataan$p\Longleftrightarrow\sim q$ dapat dinyatakan “Eka rajin belajar jika dan hanya jika ia tidak lulus ujian nasional “ -
Pertanyaan ke 2 dari 5
2. Pertanyaan
Diketahui pernyataan “ $4$ bukan bilangan komposit dan $x^{2}-1$= 0 tidak memiliki solusi jika dan hanya jika jumlah sudut dalam segitiga adalah $180\text{º}$ dapat disimbolkan dengan…
Betulmisalkan p : 4 bilangan komposit, maka $\sim p$ : 4 bukan bilangan komposit
$q :$ $x^{2}-1=0$ tmemiliki solusi, maka $\sim q:x^{2}-1=0$ tidak memiliki solusi
$r :$ jumlah sudut dalam segitiga $180\text{º}$
penghubung “dan” disimbolkan dengan “$\wedge$” dan penghubung “Jika dan hanya jika” dapat disimbolkan dengan “$\Longleftrightarrow$”
Jadi pernyataan diatas dapat disimbolkan dengan $\left(\sim p\wedge\sim q\right)\Longleftrightarrow r$Salahmisalkan p : 4 bilangan komposit, maka $\sim p$ : 4 bukan bilangan komposit
$q :$ $x^{2}-1=0$ tmemiliki solusi, maka $\sim q:x^{2}-1=0$ tidak memiliki solusi
$r :$ jumlah sudut dalam segitiga $180\text{º}$
penghubung “dan” disimbolkan dengan “$\wedge$” dan penghubung “Jika dan hanya jika” dapat disimbolkan dengan “$\Longleftrightarrow$”
Jadi pernyataan diatas dapat disimbolkan dengan $\left(\sim p\wedge\sim q\right)\Longleftrightarrow r$ -
Pertanyaan ke 3 dari 5
3. Pertanyaan
Nilai kebenaran dari pernyataan “$x^{2}-4=0$ tidak memiliki penyelesaian jika dan hanya jika ikan hidup di air” adalah$\ldots$
Betul$p :$ $x^{2}-4=0$ (salah) karena $x = 2$ atau $x = -2$ memenuhi persamaan $x^{2}-4=0$
$q :$ ikan hidup di air (benar)
$p\Longleftrightarrow q\equiv S\Longleftrightarrow B=$ Salah
Jadi pernyataan diatas bernilai salahSalah$p :$ $x^{2}-4=0$ (salah) karena $x = 2$ atau $x = -2$ memenuhi persamaan $x^{2}-4=0$
$q :$ ikan hidup di air (benar)
$p\Longleftrightarrow q\equiv S\Longleftrightarrow B=$ Salah
Jadi pernyataan diatas bernilai salah -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Diketahui pernyataan p : Ayah mendapat gaji dan q : Ia bekerja. Pernyataan $p\Longleftrightarrow q$ adalah….
Betul$p\Longleftrightarrow q$ adalah pernyataan biimpilkasi yang artinya “p jika dan hanya jika q”
Jadi pernyataan $p\Longleftrightarrow q$ adalah “Ayah mendapatkan gaji jika dan hanya jika ia bekerja”Salah$p\Longleftrightarrow q$ adalah pernyataan biimpilkasi yang artinya “p jika dan hanya jika q”
Jadi pernyataan $p\Longleftrightarrow q$ adalah “Ayah mendapatkan gaji jika dan hanya jika ia bekerja” -
Pertanyaan ke 5 dari 5
5. Pertanyaan
Diketahui pernyataan p : $x^{2}+8x-8\leq4x+13$ dan q : jumlah sisi titik sudut kubus ada 6. Agar pernyataan $p\Longleftrightarrow q$ bernilai benar, maka nilai x yang memenuhi adalah…..
Betul* $p:x^{2}+8x-8\leq4x+13$
$x^{2}+4x-21\leq0$
$(x+7)(x-3)\leq0$
$-7\leq x\leq3$
* $q$ : jumlah titik sudut kubus ada 6 (salah)
Karena pernyataan $p\Longleftrightarrow q$ harus bernilai benar dan diketahui $q$ bernilai salah, maka nilai $p$ harus bernilia salah.
Jadi pernyataan $p\Longleftrightarrow q$ bernilai benar jika nilai $x$ yang memenuhi adalah $x<-7$ atau $x>3.$
Salah* $p:x^{2}+8x-8\leq4x+13$
$x^{2}+4x-21\leq0$
$(x+7)(x-3)\leq0$
$-7\leq x\leq3$
* $q$ : jumlah titik sudut kubus ada 6 (salah)
Karena pernyataan $p\Longleftrightarrow q$ harus bernilai benar dan diketahui $q$ bernilai salah, maka nilai $p$ harus bernilia salah.
Jadi pernyataan $p\Longleftrightarrow q$ bernilai benar jika nilai $x$ yang memenuhi adalah $x<-7$ atau $x>3.$
Latihan Soal Biimplikasi (Sedang)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Jika pernyataan p bernilai benar dan q bernilai salah maka pernyataan yang bernilai salah adalah…
Betul$\sim p\leftrightarrow q$ (benar)
$\sim p\vee\sim q$ (benar)
$q\vee p$ (benar)
$\sim q\wedge p$ (benar)
$p\rightarrow q$ ( salah)
Salah$\sim p\leftrightarrow q$ (benar)
$\sim p\vee\sim q$ (benar)
$q\vee p$ (benar)
$\sim q\wedge p$ (benar)
$p\rightarrow q$ ( salah)
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Jika $p$ dan $q$ pernyataan-pernyataan yang bernilai salah, pernyataan-pernyataan dibawah ini yang benar adalah…
Betul$*\ \sim p\Rightarrow q:(B\Rightarrow S)$ jadi bernilai salah
$*\ p\wedge q:(S\wedge S)$ jadi bernilai salah
$*\ p\Leftrightarrow q:(S\Leftrightarrow S)$ jadi bernilai benar
$*\ p\vee q:(S\vee S)$ jadi bernilai salah
$*\ p\wedge\sim q:(S\wedge B)$ jadi bernilai salah
Pernyataan yang memenuhi adalah $p\Leftrightarrow q.$
Salah$*\ \sim p\Rightarrow q:(B\Rightarrow S)$ jadi bernilai salah
$*\ p\wedge q:(S\wedge S)$ jadi bernilai salah
$*\ p\Leftrightarrow q:(S\Leftrightarrow S)$ jadi bernilai benar
$*\ p\vee q:(S\vee S)$ jadi bernilai salah
$*\ p\wedge\sim q:(S\wedge B)$ jadi bernilai salah
Pernyataan yang memenuhi adalah $p\Leftrightarrow q.$
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Jika $q$ bernilai salah dan $p\Leftrightarrow q$ bernilai benar, maka pernyataan yang bernilai salah adalah…
Betul$p\Leftrightarrow q$ bernilai benar. Karena $p$ bernilai salah, maka $q$ juga bernilai salah.
 Salah
Salah$p\Leftrightarrow q$ bernilai benar. Karena $p$ bernilai salah, maka $q$ juga bernilai salah.

-
Pertanyaan ke 4 dari 5
4. Pertanyaan
Pernyataan $\left(\sim p\vee q\right)\wedge(p\vee\sim q)$ equivalen dengan pernyataan…
BetulPerhatikan tabel berikut :

Jadi pernyataan $\left(\sim p\vee q\right)\wedge(p\vee\sim q)$ equivalen dengan $p\Leftrightarrow q.$SalahPerhatikan tabel berikut :

Jadi pernyataan $\left(\sim p\vee q\right)\wedge(p\vee\sim q)$ equivalen dengan $p\Leftrightarrow q.$ -
Pertanyaan ke 5 dari 5
5. Pertanyaan
Pernyataan dibawah ini yang benar adalah…
BetulPilihan A tidak selalu menghasilkan $x+y>0$ untuk semua $\left(\forall x\right)$ dan $\left(\forall y\right)$
Pilihan B tidak selalu menghasilkan $x+y<0$ untuk semua $\left(\forall x\right)$ dan $\left(\forall y\right)$
Pilihan C tidak selalu menghasilkan $y+5>0$ untuk semua $\left(\forall y\right)$
Pilihan D $\left(\exists x\right)$ dan $\left(\forall y\right)$ akan ada yang menghasilkan $x-y=6$
Pilihan E harusnya untuk $\forall x$ nilai $x^{2}>0.$
SalahPilihan A tidak selalu menghasilkan $x+y>0$ untuk semua $\left(\forall x\right)$ dan $\left(\forall y\right)$
Pilihan B tidak selalu menghasilkan $x+y<0$ untuk semua $\left(\forall x\right)$ dan $\left(\forall y\right)$
Pilihan C tidak selalu menghasilkan $y+5>0$ untuk semua $\left(\forall y\right)$
Pilihan D $\left(\exists x\right)$ dan $\left(\forall y\right)$ akan ada yang menghasilkan $x-y=6$
Pilihan E harusnya untuk $\forall x$ nilai $x^{2}>0.$
Latihan Soal Biimplikasi (Sukar)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Nilai kebenaran dari $\sim\left(p\vee q\right)\Longleftrightarrow\left(\sim p\wedge\sim q\right)$ adalah…
Betul$\sim\left(p\vee q\right)\Longleftrightarrow\left(\sim p\wedge\sim q\right)$
$\sim\left(p\vee q\right)\Longleftrightarrow\sim\left(p\vee q\right)$

Jadi nilai kebenaran untuk $\sim\left(p\vee q\right)\Longleftrightarrow\left(\sim p\wedge\sim q\right)$ adalah BBBB.
Salah$\sim\left(p\vee q\right)\Longleftrightarrow\left(\sim p\wedge\sim q\right)$
$\sim\left(p\vee q\right)\Longleftrightarrow\sim\left(p\vee q\right)$

Jadi nilai kebenaran untuk $\sim\left(p\vee q\right)\Longleftrightarrow\left(\sim p\wedge\sim q\right)$ adalah BBBB.
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Agar pernyataan “$x^{2}-1=0$ jika hanya dan hanya jika $x^{2}+4x-5=0$” benar, maka …
BetulMisal $p=x^{2}-1=0$, $x=1$ atau $x=-1$
dan $q=x^{2}+4x-5=0$ , $x=-5$ atau $x=1$
$p\Longleftrightarrow q$ akan bernilai benar jika $p$ dan $q$ dua-duanya benar atau $p$ dan $q$ dua-duanya salah.
(1) $x=1$ (benar)
(2) $x\neq-1$ (benar)
(3) $x\neq-1$ dan $x\neq-5$ (benar)
(4) $x\neq-5$ (benar)
Jadi semua pernyataan bernilai benar.
SalahMisal $p=x^{2}-1=0$, $x=1$ atau $x=-1$
dan $q=x^{2}+4x-5=0$ , $x=-5$ atau $x=1$
$p\Longleftrightarrow q$ akan bernilai benar jika $p$ dan $q$ dua-duanya benar atau $p$ dan $q$ dua-duanya salah.
(1) $x=1$ (benar)
(2) $x\neq-1$ (benar)
(3) $x\neq-1$ dan $x\neq-5$ (benar)
(4) $x\neq-5$ (benar)
Jadi semua pernyataan bernilai benar.
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Diketahui $p,\, q,\, r,\, s$ adalah pernyataan pernyataan. Jika pernyataan berikut benar :
(1) $p\wedge q$
(2) $q\Longleftrightarrow r$
(3) $r\Longleftrightarrow s$
(4) dan $s$ benarMaka pernyataan berikut yang benar adalah…
BetulJika $s$ benar, maka $r$ benar
Jika $r$ benar, maka $q$ benar
Jika $q$ benar, maka $s$ benar
(1) $p\vee q$ (benar)
(2) $\sim p\vee q$ (benar)
(3) $p\rightarrow q$ (benar)
(4) $\sim p\rightarrow\sim s$ (benar)
SalahJika $s$ benar, maka $r$ benar
Jika $r$ benar, maka $q$ benar
Jika $q$ benar, maka $s$ benar
(1) $p\vee q$ (benar)
(2) $\sim p\vee q$ (benar)
(3) $p\rightarrow q$ (benar)
(4) $\sim p\rightarrow\sim s$ (benar)
-
Pertanyaan ke 4 dari 5
4. Pertanyaan
Pernyataan “empat bilangan genap jika dan hanya jika $2+1\geq8$” senilai dengan pernyataan…
BetulMisal $p=4$ bilangan genap, dan $q=2+1\geq8$

$p\Longleftrightarrow q\equiv\sim p\Longleftrightarrow\sim q$
Jadi pernyataan yang memenuhi adalah “empat bukan bilangan genap jika dan hanya jika $2+1<8$''.
SalahMisal $p=4$ bilangan genap, dan $q=2+1\geq8$

$p\Longleftrightarrow q\equiv\sim p\Longleftrightarrow\sim q$
Jadi pernyataan yang memenuhi adalah “empat bukan bilangan genap jika dan hanya jika $2+1<8$''.
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Negasi dari pernyataan “Suatu segitiga dikatakan sama kaki jika dan hanya jika terdapat dua buah
sudutnya sama besar” adalah…Betul$\begin{aligned}\sim(p\leftrightarrow q) & \equiv\sim p\leftrightarrow q\\
& \equiv p\leftrightarrow q
\end{aligned}
$Negasinya adalah Suatu segitiga dikatakan sama kaki jika dan hanya jika tidak terdapat dua buah sudutnya sama besar.
Salah$\begin{aligned}\sim(p\leftrightarrow q) & \equiv\sim p\leftrightarrow q\\
& \equiv p\leftrightarrow q
\end{aligned}
$Negasinya adalah Suatu segitiga dikatakan sama kaki jika dan hanya jika tidak terdapat dua buah sudutnya sama besar.