Ingin mempelajari materi fisika, khususnya tentang Gerak Lurus Berubah Beraturan? Supaya lebih paham, kamu bisa menyimak pembelajarannya di sini. Kamu juga bisa mengerjakan soal latihan untuk mempraktikkan materi yang telah dijelaskan.
Lewat pembahasan ini, kamu bisa belajar mengenai Gerak Lurus Berubah Beraturan. Kamu akan diajak untuk memahami materi dan tentang metode menyelesaikan soal.
Kamu juga akan memperoleh latihan soal interaktif yang tersedia dalam tiga tingkat kesulitan, yaitu mudah, sedang, dan sukar. Tertarik untuk mempelajarinya?
Sekarang, kamu bisa mulai mempelajari materi lewat uraian berikut. Apabila materi ini berguna, bagikan ke teman-teman kamu supaya mereka juga mendapatkan manfaatnya.
Kamu dapat download modul & kumpulan soal dalam bentuk pdf pada link dibawah ini:
Definisi
Gerak Lurus Berubah Beraturan (GLBB) adalah gerak dengan percepatan tetap.
1. Besaran Gerak Gerak Lurus Berubah Beraturan
Pengertian GLBB adalah gerak dengan percepatan tetap. Percepatan yang tetap membawa konsekuensi kecepatannya berubah secara teratur dan lintasannya lurus.
Percepatan adalah perubahan kecepatan tiap satuan waktu. Sebagai contoh jika batu dipercepat oleh percepatan gravitasi $10\mbox{ m/s}^{2}$ hal ini berarti bahwa kecepatan batu bertambah 10 m/s setiap detik.
Dalam bentuk yang lebih umum jika benda yang sedang bergerak dengan kecepatan awal $v_{0}$ kemudian dipercepat dengan percepatan sebesar $a$ selama $t$ maka kecepatan benda menjadi
\begin{equation}
v_{t}=v_{0}+at
\end{equation}
Percepatan pada gerak lurus berubah beraturan adalah suatu konstanta yang tidak berubah terhadap waktu. Berdasarkan definisi percepatan sebagai turunan pertama dari fungsi kecepatan terhadap waktu maka
\begin{equation}
\begin{alignedat}{1}dv & =a\, dt\\
v_{t} & =\intop_{0}^{t}a\mbox{ }dt+v_{0}\\
v_{t} & =at+v_{0}
\end{alignedat}
\end{equation}
Persamaan rumus GLBB (1) dan (2) adalah persamaan yang serupa. Kemudian dari rumus GLBB persamaan (2) kita dapat menentukan posisi benda yang bergerak GLBB. Karena kecepatan adalah turunan pertama dari fungsi posisi terhadap waktu maka posisi dapat ditentukan dengan mengintegralkan fungsi kecepatan terhadap waktu.
\begin{equation}
\begin{alignedat}{1}dr & =v\, dt\\
r_{t} & =\intop_{0}^{t}\left(at+v_{0}\right)\mbox{ }dt+r_{0}\\
r_{t} & =\frac{1}{2}at^{2}+v_{0}t+r_{0}
\end{alignedat}
\end{equation}
dengan $r_{t}$ adalah posisi akhir dan $r_{0}$ adalah posisi awal. Karena perpindahan $\Delta r=r_{t}-r_{0}$ maka perpindahan juga dapat dituliskan sebagai $\Delta r=\frac{1}{2}at^{2}+v_{0}t+r_{0}.$
2. Grafik Gerak Lurus Berubah Beraturan
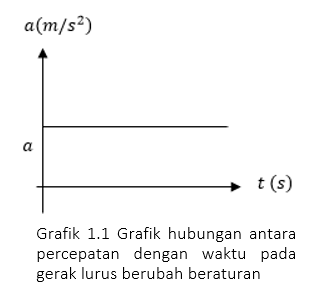
A. Grafik percepatan $(a)$ terhadap waktu ($t$)
Karena percepatannya kontsan maka grafik $a$ terhadap waktu adalah berupa garis lurus seperti gambar berikut.
B. Grafik kecepatan $(v)$ terhadap waktu $(t)$
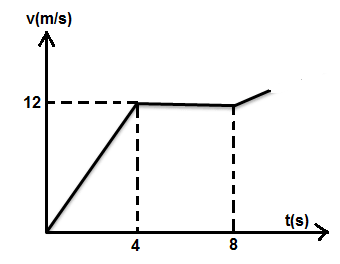
Kecepatan pada gerak lurus berubah beraturan selalu berubah terhadap waktu. Pertambahan atau pengurangan kecepatan bernilai konstan. Sehingga grafik hubungan antara $v$ dengan $t$ adalah grafik linear seperti grafik 1.2.

Melalui grafik $v$ terhadap $t$, kita dapat menentukan besar jarak dan percepatan. Jarak dapat ditentukan dengan menghitung luas daerah di bawah kurva. Percepatan dapat dihitung dengan menghitung gradien grafik $v-t.$
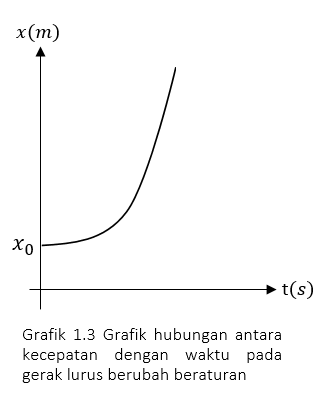
C. Grafik posisi $(x)$ terhadap waktu
Posisi merupakan fungsi kuadrat waktu, sehingga grafik posisi terhadap waktu berupa grafik fungsi kuadrat.
Contoh Soal GLBB & Penyelesaiannya
- Sebuah mobil bergerak dengan kecepatan 36 km/jam, kemudian mobil ini dipercepat dengan percepatan $1\mbox{m/s}^{2}.$ Hitunglah kecepatan dan jarak yang ditempuh selama 20 detik setelah mobil dipercepat!
Penyelesaian:
Dari soal diperoleh $v_{0}=10$ m/s; $a=1\mbox{ m/s}^{2}$ dan $t=20$ s.
a. Kecepatan
$\begin{alignedat}{1}v & =v_{0}+at\\
& =10+20\\
& =30\mbox{ m/s}
\end{alignedat}
$
b. Jarak yang ditempuh
$\begin{alignedat}{1}\Delta x & =v_{0}t+\frac{1}{2}at^{2}\\
& =10\times20+\frac{1}{2}\times1\times20^{2}\\
& =600\mbox{ m}
\end{alignedat}
$
- Hitunglah percepatan sebuah mobil yang mula-mula diam lalu dipercepat selama 8 detik dan menempuh jarak 50 meter.
Penyelesaian:
Dari soal diperoleh $v_{0}=0$ m/s; $\Delta x=50\mbox{ m}$ dan $t=8$ s.
Jarak yang ditempuh
$\begin{alignedat}{1}x & =v_{0}t+\frac{1}{2}at^{2}\\
50 & =\frac{1}{2}\times a\times8^{2}\\
a & =\frac{50}{32}\mbox{ m}\\
& =\frac{25}{16}\mbox{ m}
\end{alignedat}
$
Latihan Soal Gerak Lurus Berubah Beraturan (Mudah)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Benda mula-mula diam kemudian bergerak dengan percepatan 3 m/s$^{2}$. Berapa lama waktu yang dibutuhkan ketika benda menempuh jarak 150 m?
Betul$\begin{alignedat}{1}s & =v_{0}\cdot t+\frac{1}{2}at^{2}\\
150 & =0+\frac{1}{2}at^{2}\\
\frac{300}{3} & =t^{2}\\
t & =10\mbox{ sekon}.
\end{alignedat}
$Salah$\begin{alignedat}{1}s & =v_{0}\cdot t+\frac{1}{2}at^{2}\\
150 & =0+\frac{1}{2}at^{2}\\
\frac{300}{3} & =t^{2}\\
t & =10\mbox{ sekon}.
\end{alignedat}
$ -
Pertanyaan ke 2 dari 5
2. Pertanyaan
Benda bergerak lurus dengan percepatan tetap 2 m/s$^{2}.$ Jika kecepatan awal benda 5 m/s maka kecepatan dan jarak tempuh benda itu pada akhir detik ke-5 adalah … .
BetulKecepatan
$\begin{alignedat}{1}v_{t} & =v_{0}+at\\
& =5+2(5)\\
v_{t} & =15\mbox{ m/s}
\end{alignedat}
$Jarak tempuh
$\begin{alignedat}{1}s & =v_{0}t+\frac{1}{2}at^{2}\\
& =5(5)+\frac{1}{2}(2)(5)^{2}\\
s & =50\mbox{ m.}
\end{alignedat}
$SalahKecepatan
$\begin{alignedat}{1}v_{t} & =v_{0}+at\\
& =5+2(5)\\
v_{t} & =15\mbox{ m/s}
\end{alignedat}
$Jarak tempuh
$\begin{alignedat}{1}s & =v_{0}t+\frac{1}{2}at^{2}\\
& =5(5)+\frac{1}{2}(2)(5)^{2}\\
s & =50\mbox{ m.}
\end{alignedat}
$ -
Pertanyaan ke 3 dari 5
3. Pertanyaan
Sebuah pesawat memerlukan kecepatan minimal 30 m/s agar dapat lepas landas dari suatu landasan. Bila mesin pesawat tersebut mampu menghasilkan percepatan maksimum 1 m/s$^{2}.$ Berapakah panjang minimal lintasan/landasan agar pesawat dapat lepas landas dari keadaan berhenti … .
BetulPesawat bergerak GLBB dari keadaan diam $v_{0}=0$ sehingga
$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}+2as\\
30^{2} & =0+2(1)s\\
s & =450\mbox{ meter.}
\end{alignedat}
$SalahPesawat bergerak GLBB dari keadaan diam $v_{0}=0$ sehingga
$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}+2as\\
30^{2} & =0+2(1)s\\
s & =450\mbox{ meter.}
\end{alignedat}
$ -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Gerak suatu benda dinyatakan oleh grafik kecepatan terhadap waktu berikut ini:

Jarak yang ditempuh benda setelah bergerak selama 8 detik adalah … .
BetulJarak tempuh = luas grafik (luas trapesium)
Jarak tempuh = (8+4)$\frac{12}{2}$ = 72 m.
SalahJarak tempuh = luas grafik (luas trapesium)
Jarak tempuh = (8+4)$\frac{12}{2}$ = 72 m.
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Sebuah batu besar berada pada jarak 25 m di depan sebuah kendaraan yang bergerak dengan kecepatan 10 m/s. Agar tepat berhenti sebelum mengenai batu, maka kendaraan tersebut harus direm dengan memberikan perlambatan sebesar … m/s$^{2}.$
Betul$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}+2as\\
& =10^{2}+2a(25)\\
50a & =-100\\
a & =-2\mbox{ m/}\mbox{s}^{2}.
\end{alignedat}
$Salah$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}+2as\\
& =10^{2}+2a(25)\\
50a & =-100\\
a & =-2\mbox{ m/}\mbox{s}^{2}.
\end{alignedat}
$
Latihan Soal Gerak Lurus Berubah Beraturan (Sedang)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Sebuah mobil bergerak dengan kecepatan awal $v_{0}.$ Setelah 10 detik, mobil tersebut menempuh jarak 200 m dan kecepatan pada waktu itu adalah 25 m/s. Maka kecepatan awal $v_{0}$ adalah . . .
BetulPercepatan mobil dapat ditentukan dari persamaan menentukan jarak:
$\begin{alignedat}{1}x & =x_{0}+v_{0}t+\frac{1}{2}at^{2}\\
& =0+(v-at)t+\frac{1}{2}at^{2}\\
x & =vt-\frac{1}{2}at^{2}
\end{alignedat}
$$\begin{alignedat}{1}a & =\frac{2(vt-x)}{t^{2}}\\
a & =\frac{2(25\cdot10-200)}{10^{2}}=1\mbox{ m/}\mbox{s}^{2}
\end{alignedat}
$Sehingga kecepatan awalnya adalah
$\begin{alignedat}{1}v_{0} & =v-at\\
& =25-1\cdot10=15\mbox{ m/s}.
\end{alignedat}
$SalahPercepatan mobil dapat ditentukan dari persamaan menentukan jarak:
$\begin{alignedat}{1}x & =x_{0}+v_{0}t+\frac{1}{2}at^{2}\\
& =0+(v-at)t+\frac{1}{2}at^{2}\\
x & =vt-\frac{1}{2}at^{2}
\end{alignedat}
$$\begin{alignedat}{1}a & =\frac{2(vt-x)}{t^{2}}\\
a & =\frac{2(25\cdot10-200)}{10^{2}}=1\mbox{ m/}\mbox{s}^{2}
\end{alignedat}
$Sehingga kecepatan awalnya adalah
$\begin{alignedat}{1}v_{0} & =v-at\\
& =25-1\cdot10=15\mbox{ m/s}.
\end{alignedat}
$ -
Pertanyaan ke 2 dari 5
2. Pertanyaan
Seorang sopir mengendarai bus kota dengan kecepatan 72 km/jam. Karena sudah dekat lampu merah ia memperlambat bus tersebut. Jika jarak lampu lalu lintas tersebut 100 m, berapa perlambatan yang harus diberikan agar ia dapat tepat berhenti di depan lalu lintas tersebut ?
Betul$v_{0}=72\mbox{ km/jam}=20\mbox{ m/s}$
$v=0\mbox{ m/s}$, $x_{0}=0,$ $x=100$ m
$\begin{alignedat}{1}v & =v_{0}+at\\
t & =\frac{v-v_{0}}{a}
\end{alignedat}
$Percepatannya adalah
$\begin{alignedat}{1}x & =x_{0}+v_{0}t+\frac{1}{2}at^{2}\\
& =x_{0}+v_{0}\frac{v-v_{0}}{a}+\frac{1}{2}\cdot a\frac{(v-v_{0})^{2}}{a^{2}}=\frac{v^{2}-v_{0}^{2}}{2a}\\
a & =\frac{v^{2}-v_{0}^{2}}{2x}=\frac{0^{2}-20^{2}}{2\cdot100}=-2\mbox{ m/}\mbox{s}^{2}
\end{alignedat}
$Tanda negatif menunjukkan perlambatan.
Salah$v_{0}=72\mbox{ km/jam}=20\mbox{ m/s}$
$v=0\mbox{ m/s}$, $x_{0}=0,$ $x=100$ m
$\begin{alignedat}{1}v & =v_{0}+at\\
t & =\frac{v-v_{0}}{a}
\end{alignedat}
$Percepatannya adalah
$\begin{alignedat}{1}x & =x_{0}+v_{0}t+\frac{1}{2}at^{2}\\
& =x_{0}+v_{0}\frac{v-v_{0}}{a}+\frac{1}{2}\cdot a\frac{(v-v_{0})^{2}}{a^{2}}=\frac{v^{2}-v_{0}^{2}}{2a}\\
a & =\frac{v^{2}-v_{0}^{2}}{2x}=\frac{0^{2}-20^{2}}{2\cdot100}=-2\mbox{ m/}\mbox{s}^{2}
\end{alignedat}
$Tanda negatif menunjukkan perlambatan.
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Sebuah mobil mula-mula diam kemudian mobil dihidupkan dan mobil bergerak dengan ppercepatan tetap 2 m/s$^{2},$ setelah mobil bergerak selama 10 s mesinnya dimatikan, mobil mengalami perlambatan tetap dan mobil berhenti 10 s kemudian. Jarak yang masih ditempuh mobil mulai saat mesin dimatikan sampai berhenti adalah… .
BetulMobil mula-mula diam kemudian bergerak $a=2\mbox{ m/}\mbox{s}^{2}$ selama 10 sekon
$\begin{alignedat}{1}v_{t} & =v_{0}+at\\
& =0+2(10)\\
v_{t} & =20\mbox{ m/s}
\end{alignedat}
$lalu mesin dimatikan dan 10 detik kemudian berhenti
$\begin{alignedat}{1}v_{t} & =v_{0}+at\\
0 & =20+a(10)\\
a & =-2
\end{alignedat}
$$\begin{alignedat}{1}s & =v_{0}t+\frac{1}{2}at^{2}\\
& =20(10)+\frac{1}{2}(-2)(10)^{2}\\
s & =200-100\\
s & =100\mbox{ meter}.
\end{alignedat}
$SalahMobil mula-mula diam kemudian bergerak $a=2\mbox{ m/}\mbox{s}^{2}$ selama 10 sekon
$\begin{alignedat}{1}v_{t} & =v_{0}+at\\
& =0+2(10)\\
v_{t} & =20\mbox{ m/s}
\end{alignedat}
$lalu mesin dimatikan dan 10 detik kemudian berhenti
$\begin{alignedat}{1}v_{t} & =v_{0}+at\\
0 & =20+a(10)\\
a & =-2
\end{alignedat}
$$\begin{alignedat}{1}s & =v_{0}t+\frac{1}{2}at^{2}\\
& =20(10)+\frac{1}{2}(-2)(10)^{2}\\
s & =200-100\\
s & =100\mbox{ meter}.
\end{alignedat}
$ -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Sebuah pesawat terbang mulai bergerak dan dipercepat oleh mesinnya dengan 2,5 m/s$^{2}.$ Untuk tinggal landas (take off) pesawat terbang tersebut memerlukan kecepatan 60 m/s. Berapakah panjang landasan minimum yang diperlukan?
BetulPanjang landasan dapat dihitung dengan persamaan
$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}+2as\\
s & =\frac{v_{t}^{2}-v_{0}^{2}}{2a}\\
& =\frac{(60\mbox{ m/s})^{2}}{2(2,5\mbox{ m/}\mbox{s}^{2})}\\
s & =720\mbox{ m}.
\end{alignedat}
$SalahPanjang landasan dapat dihitung dengan persamaan
$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}+2as\\
s & =\frac{v_{t}^{2}-v_{0}^{2}}{2a}\\
& =\frac{(60\mbox{ m/s})^{2}}{2(2,5\mbox{ m/}\mbox{s}^{2})}\\
s & =720\mbox{ m}.
\end{alignedat}
$ -
Pertanyaan ke 5 dari 5
5. Pertanyaan
Kecepatan kereta api bekurang secara beraturan dari 5$\sqrt{10}$ m/s menjadi 4$\sqrt{10}$ m/s dalam jarak 45 m. Berapakah jarak yang masih dapat ditempuh kereta api itu sebelum berhenti?
Betul$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}+2as\\
a & =\frac{v_{t}^{2}-v_{0}^{2}}{2s}\\
a & =\frac{(4\sqrt{10}\mbox{ m/s})^{2}-(5\sqrt{10}\mbox{ m/s})^{2}}{2(45\mbox{ m})}\\
a & =-1\mbox{ m/}\mbox{s}^{2}
\end{alignedat}
$Negatif menunjukkan kereta mengalami perlambatan
Kereta api berhenti berarti kecepatan akhir kereta $v_{t}=0$
$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}+2as\\
s & =\frac{v_{t}^{2}-v_{0}^{2}}{2a}\\
& =\frac{0-(4\sqrt{10}\mbox{ m/s})^{2}}{2(-1\mbox{ m/}\mbox{s}^{2})}\\
s & =80\mbox{ meter}.
\end{alignedat}
$Salah$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}+2as\\
a & =\frac{v_{t}^{2}-v_{0}^{2}}{2s}\\
a & =\frac{(4\sqrt{10}\mbox{ m/s})^{2}-(5\sqrt{10}\mbox{ m/s})^{2}}{2(45\mbox{ m})}\\
a & =-1\mbox{ m/}\mbox{s}^{2}
\end{alignedat}
$Negatif menunjukkan kereta mengalami perlambatan
Kereta api berhenti berarti kecepatan akhir kereta $v_{t}=0$
$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}+2as\\
s & =\frac{v_{t}^{2}-v_{0}^{2}}{2a}\\
& =\frac{0-(4\sqrt{10}\mbox{ m/s})^{2}}{2(-1\mbox{ m/}\mbox{s}^{2})}\\
s & =80\mbox{ meter}.
\end{alignedat}
$
Latihan Soal Gerak Lurus Berubah Beraturan (Sukar)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Sebuah mobil balap direm dengan perlambatan konstan dari kelajuan 25 m/s menjadi 15 m/s dalam jarak 40 m. Jarak total (dalam meter) yang telah ditempuh oleh mobil tersebut sampai berhenti adalah… .
BetulDari $v_{1}=25$ m/s ke $v_{2}=15$ m/s menempuh jarak 40 m maka
$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}-2as\\
15^{2} & =25^{2}-2(a)(40)\\
225 & =625-80a\\
80a & =400\\
a & =5\mbox{ m/}\mbox{s}^{2}
\end{alignedat}
$Jarak total dari $v_{1}=25$ m/s ke $v_{3}=0$ yaitu
$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}-2as\\
0 & =25^{2}-2(5)(s)\\
10s & =625\\
s & =62,5\mbox{ meter.}
\end{alignedat}
$SalahDari $v_{1}=25$ m/s ke $v_{2}=15$ m/s menempuh jarak 40 m maka
$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}-2as\\
15^{2} & =25^{2}-2(a)(40)\\
225 & =625-80a\\
80a & =400\\
a & =5\mbox{ m/}\mbox{s}^{2}
\end{alignedat}
$Jarak total dari $v_{1}=25$ m/s ke $v_{3}=0$ yaitu
$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}-2as\\
0 & =25^{2}-2(5)(s)\\
10s & =625\\
s & =62,5\mbox{ meter.}
\end{alignedat}
$ -
Pertanyaan ke 2 dari 5
2. Pertanyaan
Sebuah partikel mengalami perlambatan kostan sehingga kecepatannya berubah 20 m/s menjadi 10 m/s setelah menempuh jarak 75 meter. Maka total jarak yang ditempuh partikel tersebut sampai berhenti adalah… .
Betul$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}+2as\\
10^{2} & =20^{2}+2a\times75\\
100 & =400+150a\\
-300 & =150a\\
a & =-2\mbox{ m/}\mbox{s}^{2}
\end{alignedat}
$$\begin{alignedat}{1}v_{t} & =v_{0}+at\\
0 & =10-2t\\
t & =\frac{10}{2}\mbox{ sekon}
\end{alignedat}
$$\begin{alignedat}{1}s & =v_{0}\cdot t+\frac{1}{2}at^{2}\\
& =(10)(5)+\frac{1}{2}(-2)(5)^{2}\\
s & =50-25\\
s & =25\mbox{ meter}
\end{alignedat}
$Total jarak yang ditempuh oleh partikel adalah 75 m + 25 m = 100 m.
Salah$\begin{alignedat}{1}v_{t}^{2} & =v_{0}^{2}+2as\\
10^{2} & =20^{2}+2a\times75\\
100 & =400+150a\\
-300 & =150a\\
a & =-2\mbox{ m/}\mbox{s}^{2}
\end{alignedat}
$$\begin{alignedat}{1}v_{t} & =v_{0}+at\\
0 & =10-2t\\
t & =\frac{10}{2}\mbox{ sekon}
\end{alignedat}
$$\begin{alignedat}{1}s & =v_{0}\cdot t+\frac{1}{2}at^{2}\\
& =(10)(5)+\frac{1}{2}(-2)(5)^{2}\\
s & =50-25\\
s & =25\mbox{ meter}
\end{alignedat}
$Total jarak yang ditempuh oleh partikel adalah 75 m + 25 m = 100 m.
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Sebuah partikel bergerak lurus dengan kecepatan $v=2t^{3}+3t^{2}-9$ (dalam m/s) dan $t$ dalam detik. Pada waktu $t=2$ detik partikel ini berada pada posisi s = 6 meter. Hitung posisi dan percepatan partikel pada waktu $t=3$ detik.
Betul$\begin{alignedat}{1}s & =s_{0}+\int_{2}^{3}v\cdot dt\\
s_{3} & =s_{2}+\int_{2}^{3}v\cdot dt\\
& =6+\int_{2}^{3}(2t^{3}+3t^{2}-9)\cdot dt\\
& =6+(\frac{1}{2}t^{4}+t^{3}-9t)]_{2}^{3}\\
& =6+(\frac{1}{2}3^{4}+3^{3}-9\cdot3)-(\frac{1}{2}2^{4}+2^{3}-9\cdot2)\\
& =6+(40,5)-(-2)\\
s & =48,5\mbox{ meter}
\end{alignedat}
$Percepatan partikel
$\begin{alignedat}{1}a_{t} & =\frac{dv}{dt}\\
& =\frac{d}{dt}(2t^{3}+3t^{2}-9)\\
& =6t^{2}+6t\\
a_{3} & =6\cdot3^{3}+6\cdot3\\
a_{3} & =72\mbox{ m/}\mbox{s}^{2}.
\end{alignedat}
$Salah$\begin{alignedat}{1}s & =s_{0}+\int_{2}^{3}v\cdot dt\\
s_{3} & =s_{2}+\int_{2}^{3}v\cdot dt\\
& =6+\int_{2}^{3}(2t^{3}+3t^{2}-9)\cdot dt\\
& =6+(\frac{1}{2}t^{4}+t^{3}-9t)]_{2}^{3}\\
& =6+(\frac{1}{2}3^{4}+3^{3}-9\cdot3)-(\frac{1}{2}2^{4}+2^{3}-9\cdot2)\\
& =6+(40,5)-(-2)\\
s & =48,5\mbox{ meter}
\end{alignedat}
$Percepatan partikel
$\begin{alignedat}{1}a_{t} & =\frac{dv}{dt}\\
& =\frac{d}{dt}(2t^{3}+3t^{2}-9)\\
& =6t^{2}+6t\\
a_{3} & =6\cdot3^{3}+6\cdot3\\
a_{3} & =72\mbox{ m/}\mbox{s}^{2}.
\end{alignedat}
$ -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Partikel partikel A bergerak dari titik P ke titik Q melalui lintasan lurus dipercepat dengan percepatan 5 m/s$^{2}.$ Mula-mula A diam. Partikel B pada waktu yang sama bergerak dipercepat juga dari titik Q dengan arah yang sama dengan gerak partikel A dan besarnya 1 m/s$^{2}.$ Kecepatan mula-mula partikel B 10 m/s. Jika jarak PQ = 100 m. Dimanakah kedua partikel tersebut bertemu bila diukur dari titik P dimana A mulai bergerak?
BetulKarena partikel A dan B berangkat bersama-sama maka $t_{A}=t_{B}=t$
Partikel A
$x_{0}=0,$ $v_{0}=0,$ $a=5\mbox{ m/}\mbox{s}^{2}$
Partikel B
$x_{0}=100\mbox{ meter},$ $v_{0}=10\mbox{ m/s},$ $a=1\mbox{ m/}\mbox{s}^{2}$
$\begin{alignedat}{1}x_{A} & =x_{B}\\
(x_{0})_{A}+(v_{0})_{A}\cdot t_{A}+\frac{1}{2}\cdot a_{A}\cdot t_{A}^{2} & =(x_{0})_{B}+(v_{0})_{B}\cdot t_{B}+\frac{1}{2}\cdot a_{B}t_{B}^{2}\\
0+0\cdot t+\frac{1}{2}\cdot5\cdot t^{2} & =100+10\cdot t+\frac{1}{2}\cdot1\cdot t^{2}\\
\frac{1}{2}\cdot5\cdot t^{2} & =100+10\cdot t+\frac{1}{2}\cdot1\cdot t^{2}\\
2t^{2}-10t-100 & =0\\
t^{2}-5t-50 & =0\\
(t+5)(t-10) & =0\\
t_{1} & =-5\mbox{ s}\\
t_{2} & =10\mbox{ s}
\end{alignedat}
$Gunakan waktu positif. Karena waktu tidak pernah negatif.
Posisi partikel ketika bertemu setelah 10 detik
$\begin{alignedat}{1}x_{A} & =(x_{0})_{A}+(v_{0})_{A}\cdot t_{A}+\frac{1}{2}\cdot a_{A}\cdot t_{A}^{2}\\
& =0+0+\frac{1}{2}\cdot5\cdot10^{2}\\
x_{A} & =250\mbox{ meter}
\end{alignedat}
$Jarak ini diukur dari titik P dimana A mulai bergerak.
SalahKarena partikel A dan B berangkat bersama-sama maka $t_{A}=t_{B}=t$
Partikel A
$x_{0}=0,$ $v_{0}=0,$ $a=5\mbox{ m/}\mbox{s}^{2}$
Partikel B
$x_{0}=100\mbox{ meter},$ $v_{0}=10\mbox{ m/s},$ $a=1\mbox{ m/}\mbox{s}^{2}$
$\begin{alignedat}{1}x_{A} & =x_{B}\\
(x_{0})_{A}+(v_{0})_{A}\cdot t_{A}+\frac{1}{2}\cdot a_{A}\cdot t_{A}^{2} & =(x_{0})_{B}+(v_{0})_{B}\cdot t_{B}+\frac{1}{2}\cdot a_{B}t_{B}^{2}\\
0+0\cdot t+\frac{1}{2}\cdot5\cdot t^{2} & =100+10\cdot t+\frac{1}{2}\cdot1\cdot t^{2}\\
\frac{1}{2}\cdot5\cdot t^{2} & =100+10\cdot t+\frac{1}{2}\cdot1\cdot t^{2}\\
2t^{2}-10t-100 & =0\\
t^{2}-5t-50 & =0\\
(t+5)(t-10) & =0\\
t_{1} & =-5\mbox{ s}\\
t_{2} & =10\mbox{ s}
\end{alignedat}
$Gunakan waktu positif. Karena waktu tidak pernah negatif.
Posisi partikel ketika bertemu setelah 10 detik
$\begin{alignedat}{1}x_{A} & =(x_{0})_{A}+(v_{0})_{A}\cdot t_{A}+\frac{1}{2}\cdot a_{A}\cdot t_{A}^{2}\\
& =0+0+\frac{1}{2}\cdot5\cdot10^{2}\\
x_{A} & =250\mbox{ meter}
\end{alignedat}
$Jarak ini diukur dari titik P dimana A mulai bergerak.
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Partikel partikel A bergerak dari titik P ke titik Q melalui lintasan lurus dipercepat dengan percepatan 5 m/s$^{2}.$ Mula-mula A diam. Partikel B pada waktu yang sama bergerak dipercepat juga dari titik Q menuju titik P sebesar 1 m/s$^{2}.$ Kecepatan mula-mula partikel B 10 m/s berangkat 8 detik lebih dahulu. Jika jarak PQ = 160 m. Dimanakah kedua partikel tersebut bertemu bila diukur dari titik P dimana A mulai bergerak?
BetulKarena B berangkat 8 detik lebih dahulu maka $t_{B}=t_{A}+8.$ Kecepatan dan percepatan B harus diberi tanda negatif karena arahnya kekiri.
$\begin{alignedat}{1}x_{A} & =x_{B}\\
(x_{0})_{A}+(v_{0})_{A}\cdot t_{A}+\frac{1}{2}\cdot a_{A}\cdot t_{A}^{2} & =(x_{0})_{B}+(v_{0})_{B}\cdot t_{B}+\frac{1}{2}\cdot a_{B}\cdot t_{B}^{2}\\
0\cdot t+\frac{1}{2}\cdot5\cdot t_{A}^{2} & =160-10\cdot(t_{A}+8)-\frac{1}{2}\cdot1(t_{A}+8)^{2}\\
\frac{1}{2}\cdot5\cdot t_{A}^{2} & =160-10\cdot t_{A}-80-\frac{1}{2}(t_{A}^{2}+16t_{A}+64)\\
3t_{A}^{2}+18t_{A}-48 & =0\\
t_{A}+6t_{A}-48 & =0\\
(t_{A}-2)(t_{A}+8) & =0\\
t_{1} & =-8\mbox{ s}\\
t_{2} & =2\mbox{ s}
\end{alignedat}
$Karena waktu tidak ada negatif maka kita ambil yang positif. Jadi
mereka bertemu 2 detik setelah A berangkat. Posisi letak partikel
itu ketika bertemu dapat dicari sebagai berikut:$\begin{alignedat}{1}x_{A} & =(x_{0})_{A}+(v_{0})_{A}\cdot t_{A}+\frac{1}{2}\cdot a_{A}\cdot t_{A}^{2}\\
& =0+0+\frac{1}{2}\cdot5\cdot2^{2}\\
& =10\mbox{ meter}
\end{alignedat}
$Jarak ini diukur dari titik P dimana A mulai bergerak.
SalahKarena B berangkat 8 detik lebih dahulu maka $t_{B}=t_{A}+8.$ Kecepatan dan percepatan B harus diberi tanda negatif karena arahnya kekiri.
$\begin{alignedat}{1}x_{A} & =x_{B}\\
(x_{0})_{A}+(v_{0})_{A}\cdot t_{A}+\frac{1}{2}\cdot a_{A}\cdot t_{A}^{2} & =(x_{0})_{B}+(v_{0})_{B}\cdot t_{B}+\frac{1}{2}\cdot a_{B}\cdot t_{B}^{2}\\
0\cdot t+\frac{1}{2}\cdot5\cdot t_{A}^{2} & =160-10\cdot(t_{A}+8)-\frac{1}{2}\cdot1(t_{A}+8)^{2}\\
\frac{1}{2}\cdot5\cdot t_{A}^{2} & =160-10\cdot t_{A}-80-\frac{1}{2}(t_{A}^{2}+16t_{A}+64)\\
3t_{A}^{2}+18t_{A}-48 & =0\\
t_{A}+6t_{A}-48 & =0\\
(t_{A}-2)(t_{A}+8) & =0\\
t_{1} & =-8\mbox{ s}\\
t_{2} & =2\mbox{ s}
\end{alignedat}
$Karena waktu tidak ada negatif maka kita ambil yang positif. Jadi
mereka bertemu 2 detik setelah A berangkat. Posisi letak partikel
itu ketika bertemu dapat dicari sebagai berikut:$\begin{alignedat}{1}x_{A} & =(x_{0})_{A}+(v_{0})_{A}\cdot t_{A}+\frac{1}{2}\cdot a_{A}\cdot t_{A}^{2}\\
& =0+0+\frac{1}{2}\cdot5\cdot2^{2}\\
& =10\mbox{ meter}
\end{alignedat}
$Jarak ini diukur dari titik P dimana A mulai bergerak.