Kamu dapat download modul & kumpulan soal dalam bentuk pdf pada link dibawah ini:

• Modul Hukum Kepler
• Kumpulan Soal Mudah, Sedang & Sukar

Definisi Hukum Kepler

Sejarah telah banyak mencatat tentang pengamatan manusia terhadap pergerakan benda-benda langit. Salah satu ilmuan yang terkenal adalah ilmuwan Jerman Johannes Kepler. Kepler menyimpulkan hasil pengamatannya melalui hukum yang ditulis sebagai hukum Kepler.

Berdasarkan kalkulasi Kepler terhadap pergerakan planet, dia menyimpulkan tiga hukum berikut yang dikenal sebagai Bunyi Hukum Kepler 1, 2, dan 3.

• Semua planet bergerak di lintasan elips dengan Matahari berada di salah satu fokusnya.
• Vektor radial yang digambarkan dari Matahari ke planet menyapu area yang sama dalam interval waktu yang sama.
• Kuadrat periode planet sebanding dengan pangkat tiga semi mayor aksis dari lintasan elips. Hukum ketiga ini juga bisa disederhanakan sebagai “Kuadrat periode planet sebanding dengan pangkat tiga jari-jari lintasannya”.

A. Hukum Kepler 1

Ilmuwan pada mulanya menganggap bahwa lintasan planet berupa lingkaran, sampai akhirnya Johannes Kepler menyimpulkan bahwa lintasan melingkar hanyalah kasus-kasus tertentu saja, sedangkan secara umum lintasan planet berbentuk elips.

Untuk mempermudah membayangkan seperti apa lintasan elips, kita bisa menggambar lintasan elips dengan pertama kali menentukan dua fokus elips. Kemudian menggambar kurva dengan jarak $r_{1}$ dan $r_{2}$dari masing-masing fokus dengan jumlah $r_{1}+r_{2}$adalah nilai yang konstan (perhatikan gambar berikut).

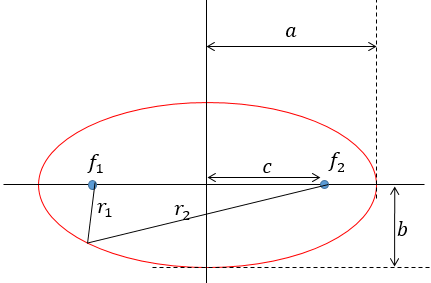
Jarak terjauh melalui pusat elips dan dua fokusnya disebut aksis mayor yaitu sepanjang $2a$ dengan $a$ disebut semi mayor aksis. Jarak terdekat melalu pusat elips disebut minor aksis yaitu sepanjang $2b$ dengan $b$ disebut semi minor aksis. Jika jarak fokus ke pusat elips adalah $c$ maka hubungan antara $a$, $b$ dan $c$ dituliskan sebagai persamaan elips sebagai berikut.

\begin{equation}
a^{2}=b^{2}+c^{2}
\end{equation}

Eccentricity dari elips didefinisikan sebagai $e=\frac{c}{a}$. Nilai eccentricity menjelaskan bentuk umum dari elips. Untuk lingkaran $c=0,$ maka nilai $e=0.$ Rentang nilai $e$ untuk elips adalah $0<e<1$.

Nilai $e$ untuk semua planet sangatlah beragam. Nilai $e$ untuk lintasan bumi adalah 0,017 yang membuat lintasan Bumi sangat menyerupai lingkaran.

Nilai $e$ terbesar dari delapan planet adalah miliki Mars, yaitu sebesar 0,21. Lintasan paling elips yang diketahu sampai saat ini adalah lintasan dari komet Halley dengan $e=0,97.$

Berikut adalah gambar (a) lintasan elips dengan nilai $e=0,21$ (planet Mars) dan (b) $e=0,97$ (Komet Halley). Gambar ini diambil dari buku Physics karangan Serway-Jewett edisi 9)

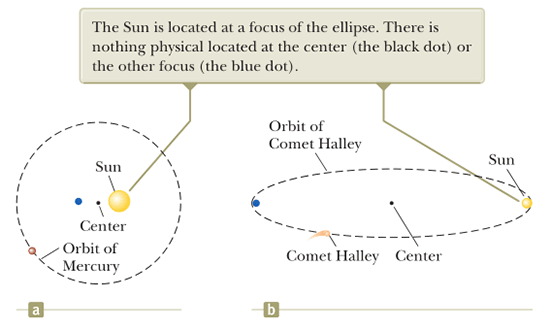
Jarak Matahri dengan planet terjauh adalah $a+c,$ titik ini disebut sebagai Aphelium (Aphelion). Jarak terdekat Planet ke Matahari adalah $a-c,$ titik ini disebut sebagai perihelium (perihelion).

B. Hukum Kepler 2

Hukum kedua ini adalah konsekuensi dari planet yang bergerak dalam sistem yang terisolasi, yaitu momentum sudutnya konstan. Jika planet bermassa $M$ bergerak dengan kecepatan $\mathbf{v}$ pada lintasan berjari-jari $\mathbf{r}$ maka momentum sudut planet adalah $\mathbf{L}$.

\begin{equation}
\mathbf{L}=M|\mathbf{\overrightarrow{r}\times}\mathbf{\overrightarrow{v}}|
\end{equation}

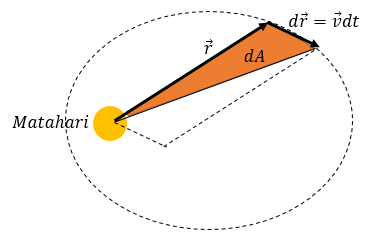
Jika pada rentang waktu $dt$ luas area yang disapu oleh vektor $\mathbf{\vec{r}}$ adalah $dA,$ maka luas $dA$ adalah setengah dari perkalian $\mathbf{\vec{r}}\times d\vec{\mathbf{r}}$, dengan mensubstitusi $d\mathbf{\vec{r}}=\mathbf{\overrightarrow{v}}dt$
maka:

\begin{equation}
dA=\frac{1}{2}|\mathbf{\vec{r}}\times d\mathbf{\vec{r}}|=\frac{1}{2}|\mathbf{\overrightarrow{r}\times\overrightarrow{v}|}dt
\end{equation}

dengan mensubstitusi persamaan (2) maka diperoleh

\begin{eqnarray}
dA & = & \frac{1}{2}\frac{L}{M}dt\nonumber \\
\frac{dA}{dt} & = & \frac{L}{2M}
\end{eqnarray}

Karena nilai $L$ dan $M$ adalah konstan, hasil ini menunjukkan bahwa turunan pertama dari fungsi luas terhadap waktu adalah konstan, artinya untuk interval waktu yang sama, area yang disapu oleh vektor jari-jari planet terhadap matahari adalah sama.

C. Hukum Kepler 3

Hukum ketiga Kepler adalah konsekuensi dari resultan gaya dari benda yang bergerak melingkar tidaklah nol, melainkan sebesar gaya sentripetalnya. Jika sebuah planet bermassa $m$ mengelilingi matahari dengan jari-jari lintasan $R$ dan karena tidak ada interaksi gaya selain gaya gravitasi, maka

\begin{eqnarray}
G\frac{Mm}{R^{2}} & = & \frac{mv^{2}}{R}\nonumber \\
G\frac{M}{R^{2}} & = & \frac{4\pi^{2}R}{T^{2}}\nonumber \\
\frac{T^{2}}{R^{3}} & = & \frac{4\pi^{2}}{GM}=2,97\times10^{-19}\mbox{s}^{2}/\mbox{m}^{3}
\end{eqnarray}

Berdasarkan persamaan (5) jelas terlihat bahwa kuadrat periode sebanding dengan pangkat tiga jari-jati lintasan planet.

Contoh Soal Hukum Kepler & Pembahasan

1. Periode Bumi mengelilingi matahari adalah 1 tahun dan periode Jupiter adalah sekitar 12 tahun. Jarak Planet Jupiter ke matahari adalah…..

Penyelesaian:

$\begin{alignedat}{1}\frac{T_{B}^{2}}{R_{B}^{3}} & =\frac{T_{J}^{2}}{R_{J}^{3}}\\
R_{J} & =\left(\frac{R_{B}^{3}}{T_{B}^{2}}\times T_{J}^{2}\right)^{\frac{1}{3}}\\
& =R_{B}\times\left(\frac{144}{1}\right)^{\frac{1}{3}}\\
& =5,24R_{\mathbf{B}}
\end{alignedat}
$

2. Asumsikan jarak bulan ke Bumi adalah $3,84\times10^{8}$ meter dan periode bulan mengelilingi Bumi adalah $2,5\times10^{6}$ s. Hitung massa Bumi!

Penyelesaian:

Berdasarkan persamaan (5) maka

$\begin{alignedat}{1}M & =\frac{4\pi^{2}R^{3}}{GT^{2}}\\
& =\frac{4\pi^{2}\times(3,84\times10^{8})^{3}}{6,674\times10^{-11}\times\left(2,5\times10^{6}\right)^{2}}\\
& =5,36\times10^{24}\mbox{kg}
\end{alignedat}
$