Apa itu Usaha Oleh Gaya Tak Konstan? Penasaran ingin mengetahuinya? Simak penjelasan lengkapnya di sini! Kami juga telah menyediakan soal atau kuis dengan tingkat kesulitan yang berbeda sebagai latihan.
Lewat pembahasan ini, kamu bisa belajar mengenai Usaha Oleh Gaya Tak Konstan. Kamu akan diajak untuk memahami materi dan tentang metode menyelesaikan soal.
Kamu juga akan memperoleh latihan soal interaktif yang tersedia dalam tiga tingkat kesulitan, yaitu mudah, sedang, dan sukar. Tertarik untuk mempelajarinya?
Sekarang, kamu bisa mulai mempelajari materi lewat uraian berikut. Apabila materi ini berguna, bagikan ke teman-teman kamu supaya mereka juga mendapatkan manfaatnya.
Kamu dapat download modul & kumpulan soal usaha oleh gaya tak konstan dalam bentuk pdf pada link dibawah ini:
Definisi
Pada pengertian usaha oleh gaya tak konstan, besar gaya yang bekerja pada suatu objek tidak selalu konstan. Beberapa gaya dipengaruhi oleh jarak seperti gaya pegas, gaya coulomb dan gaya gravitasi. Ada juga gaya yang dipengaruhi oleh kecepatan seperti gaya hambat fluida. Pada bagian ini dibahas tentang materi usaha yang diakibatkan oleh gaya-gaya tak konstan yaitu konsep usaha oleh gaya yang berubah terhadap jarak.
Usaha oleh Gaya tak Konstan
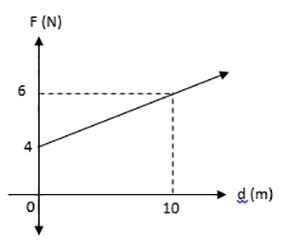
Jika gaya yang bekerja pada suatu objek merupakan fungsi jarak atau perpindahan $F(x)$ maka besar gaya berubah setiap saat terhadap jarak. Untuk menentukan besar rumus usaha yang dilakukan maka harus mengalikan gaya yang bekerja setiap saat dengan jarak yang ditempuh setiap saat pula kemudian dijumlahkan. Misalkan besar gaya yang berubah terhadap jarak dapat digambarkan seperti grafik berikut. Gaya bekerja dari jarak $x=x_{i}$ hingga $x=x_{f}.$
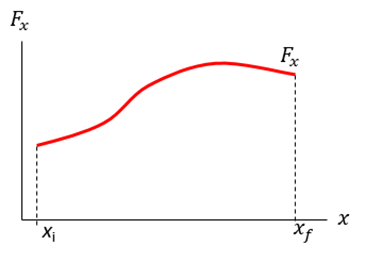
Besar usaha yang dilakukan dapat dihittung dengan menghitung luas daerah di bawah kurva. Untuk mempermudah menghitung luas daerah dibawah kurva, terlebih dahulu bagi area di bawah kurva menjadi bagian-bagian yang kecil seperti grafik berikut. Misalkan bagian terkecil memiliki lebar $dx$ dan tinggi $F_{x}$ maka pembagian ini menghasilkan bagian-bagian kecil dengan luas $dA=F_{x}dx=dW.$
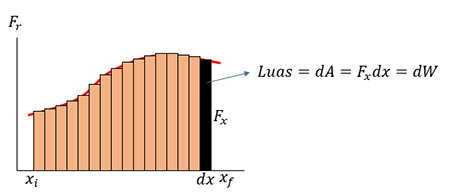
Luas yang terbentuk ini merupakan contoh usaha yang dilakukan oleh gaya untuk jarak sejauh $dx.$
\begin{equation}
dW=F_{x}dx
\end{equation}
Usaha total dapat ditentukan dengan mengintegralkan persamaan (1) dengan batas $x_{i}$ hingga $x_{f}.$
\begin{equation}
W=\intop F_{x}dx
\end{equation}
Contoh Soal & Pembahasan
- Salah bentuk gaya yang merupakan fungsi jarak adalah gaya pegas $F=-kx$ dengan $k$ disebut sebagai konstanta pegas. Tentukan usaha yang dibutuhkan untuk meregangkan pegas dari sepanjang $x_{i}$ hingga menjadi sepanjang $x_{f}!$
Penyelesaian:
Usaha yang dibutuhkan adalah
$\begin{alignedat}{1}W & =\intop_{x_{i}}^{x_{f}}-kxdx\\
W & =\left[-\frac{1}{2}kx^{2}\right]_{x_{i}}^{x_{f}}\\
W & =\frac{1}{2}k(x_{i}^{2}-x_{f}^{2})
\end{alignedat}
$
- Gaya yang bekerja pada objek digambarkan sebagai grafik $F-x$ seperti gambar berikut.
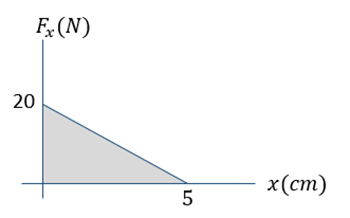
Hitung usaha yang dilakukan oleh gaya tersebut.
Penyelesaian:
Usaha yang dilakukan adalah
$\begin{alignedat}{1}W & =\mbox{luas segitiga}\\
W & =\frac{1}{2}\times5\times10^{-2}\times20\\
W & =5\times10^{-1}\mbox{N}
\end{alignedat}
$
Latihan Soal Usaha Gaya Tak Konstan (Mudah)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Pada grafik gaya terhadap perpindahan, besar usaha oleh gaya F dapat dihitung dengan cara… .
BetulUsaha dapat dihitung dengan menghitung luas area di bawah kurva yang terbentuk.
SalahUsaha dapat dihitung dengan menghitung luas area di bawah kurva yang terbentuk.
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Gaya yang bekerja pada suatu partikel dan perpindahan yang terjadi digambarkan pada grafik berikut.

Usaha yang dilakukan oleh gaya tersebut adalah… .Betul$\begin{alignedat}{1}W & =F\times d\\
& =2\times1\\
& =2\mbox{ J.}
\end{alignedat}
$Salah$\begin{alignedat}{1}W & =F\times d\\
& =2\times1\\
& =2\mbox{ J.}
\end{alignedat}
$ -
Pertanyaan ke 3 dari 5
3. Pertanyaan
Perhatikan grafik gaya terhadap perpindahan berikut.

Besar usaha yang dilakukan saat partikel mengalami perpindahan 12 meter adalah… .BetulUsaha dapat dihitung dengan menghitung luas di bawah grafik $F-d$, yaitu
$\begin{alignedat}{1}W & =\mbox{luas trapesium}\\
& =\frac{1}{2}\times\left(5+3\right)\times12\\
& =48\mbox{ J}
\end{alignedat}
$SalahUsaha dapat dihitung dengan menghitung luas di bawah grafik $F-d$, yaitu
$\begin{alignedat}{1}W & =\mbox{luas trapesium}\\
& =\frac{1}{2}\times\left(5+3\right)\times12\\
& =48\mbox{ J}
\end{alignedat}
$ -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Perhatikan grafik gaya ($F$) terhadap perpindahan $(d)$ berikut.

Gaya yang mungkin memiliki grafik tersebut adalah… .BetulPada grafik terlihat bahwa gayanya bernilai negatif kemudian menjadi nol pada titik tertentu. Gaya yang mungkin adalah gaya gesek. Gaya gesek bernilai negatif karena gaya ini berlawanan arah dengan perpindahannya, dan pada titik tertentu saat kecepatannya telah mencapai kecepatan terminal, gaya geseknya sangat kecil atau mendekati nol.
SalahPada grafik terlihat bahwa gayanya bernilai negatif kemudian menjadi nol pada titik tertentu. Gaya yang mungkin adalah gaya gesek. Gaya gesek bernilai negatif karena gaya ini berlawanan arah dengan perpindahannya, dan pada titik tertentu saat kecepatannya telah mencapai kecepatan terminal, gaya geseknya sangat kecil atau mendekati nol.
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Perhatikan grafik gaya terhadap perpindahan berikut.

Besar usaha yang dilakukan saat partikel mengalami perpindahan 6 meter adalah… .BetulUsaha dapat dihitung dengan menghitung luas di bawah grafik $F-d$, yaitu
$\begin{alignedat}{1}W & =\mbox{luas trapesium}\\
& =\frac{1}{2}\left(6+4\right)\times5\\
& =25\mbox{ J.}
\end{alignedat}
$SalahUsaha dapat dihitung dengan menghitung luas di bawah grafik $F-d$, yaitu
$\begin{alignedat}{1}W & =\mbox{luas trapesium}\\
& =\frac{1}{2}\left(6+4\right)\times5\\
& =25\mbox{ J.}
\end{alignedat}
$
Latihan Soal Usaha Gaya Tak Konstan (Sedang)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Berdasarkan grafik-grafik berikut, usaha yang dilakukan oleh gaya $F$ pada jarak $x$ memilliki nilai usaha terbesar ditunjukkan oleh grafik… .
 Betul
BetulUsaha terbesar ditunjukkan oleh grafik dengan luas area di bawah grafik $F-d$ terbesar.
SalahUsaha terbesar ditunjukkan oleh grafik dengan luas area di bawah grafik $F-d$ terbesar.
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Perhatikan grafik gaya ($F$) terhadap perpindahan $(d)$ berikut.

Usaha yang dilakukan oleh gaya $F$ jika perpindahannya 20 meter adalah… .BetulBerdasarkan grafik, maka besar gaya merupakan fungsi jarak:
$F=\left(0,2x+4\right)\mbox{ N}$, Jadi besar usaha untuk $x=0\mbox{ hingga x=20}$ m adalah
$\begin{alignedat}{1}W & =\intop_{0}^{20}\left(0,2x+4\right)\mbox{dx}\\
& =0,1x^{2}+4x|_{0}^{20}\\
& =120\mbox{ J}.
\end{alignedat}
$SalahBerdasarkan grafik, maka besar gaya merupakan fungsi jarak:
$F=\left(0,2x+4\right)\mbox{ N}$, Jadi besar usaha untuk $x=0\mbox{ hingga x=20}$ m adalah
$\begin{alignedat}{1}W & =\intop_{0}^{20}\left(0,2x+4\right)\mbox{dx}\\
& =0,1x^{2}+4x|_{0}^{20}\\
& =120\mbox{ J}.
\end{alignedat}
$ -
Pertanyaan ke 3 dari 5
3. Pertanyaan
Perhatikan grafik gaya ($F$) terhadap perpindahan $(d)$ berikut. Jika usaha total yang dilakukan oleh gaya adalah 52 J, maka nilai X yang memenuhi adalah… .
 Betul
Betul$\begin{alignedat}{1}W & =\frac{1}{2}X\times8\\
4x & =52\\
x & =13\mbox{ meter.}
\end{alignedat}
$Salah$\begin{alignedat}{1}W & =\frac{1}{2}X\times8\\
4x & =52\\
x & =13\mbox{ meter.}
\end{alignedat}
$ -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Gaya sebagai fungsi posisi dituliskan sebagai $F(r)=3r^{2}$ N. Usaha yang dilakukan oleh gaya tersebut jika gaya bekerja pada selang $r=0\mbox{ m}$ hingga $r=3$ m adalah… .
Betul$W=\intop_{0}^{3}\left(3r^{2}\right)\mbox{dr}$ $=r^{3}|_{0}^{3}$ $=27\mbox{ J}.$
Salah$W=\intop_{0}^{3}\left(3r^{2}\right)\mbox{dr}$ $=r^{3}|_{0}^{3}$ $=27\mbox{ J}.$
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Perhatikan grafik gaya ($F$) terhadap perpindahan $(x)$ berikut.

Besar usaha yang dilakukan oleh gaya pada rentang $x=0$ sampai $x=c$ adalah… .BetulBesar usaha yang dilakukan oleh gaya pada rentang $x=0$ sampai $x=c$ adalah luas grafik pada rentang tersebut. Area di bawah grafik berbentuk trapesium sehingga usahanya sebesar $\frac{1}{2}(a+b)c$.
SalahBesar usaha yang dilakukan oleh gaya pada rentang $x=0$ sampai $x=c$ adalah luas grafik pada rentang tersebut. Area di bawah grafik berbentuk trapesium sehingga usahanya sebesar $\frac{1}{2}(a+b)c$.
Latihan Soal Usaha Gaya Tak Konstan (Sukar)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Grafik gaya ($F$) yang bekerja pada sebuah partikel terhadap perpindahannya $(d)$ digambarkan sebagai berikut.

Besar usaha oleh gaya $F$ pada selang $d=0\mbox{ m}$ sampai dengan $d=3\mbox{ m}$ adalah… .BetulBerdasarkan grafik diperoleh $k=1$, sehingga usaha untuk selang $d=0\mbox{ m}$ sampai dengan $d=3\mbox{ m}$adalah $W=\intop_{0}^{3}\left(x^{2}\right)\mbox{dx}$ $=\frac{1}{3}x^{3}|_{0}^{3}$ $=3\mbox{ J}.$
SalahBerdasarkan grafik diperoleh $k=1$, sehingga usaha untuk selang $d=0\mbox{ m}$ sampai dengan $d=3\mbox{ m}$adalah $W=\intop_{0}^{3}\left(x^{2}\right)\mbox{dx}$ $=\frac{1}{3}x^{3}|_{0}^{3}$ $=3\mbox{ J}.$
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Gaya yang bekerja pada sebuah partikel memenuhi fungsi perpindahan $F(r)=\frac{k}{r^{2}}$. Usaha oleh gaya tersebut pada selang $r=k$ sampai $r=2k$ adalah… .
Betul$\begin{alignedat}{1}W & =\intop_{k}^{2k}\left(\frac{k}{r^{2}}\right)\mbox{dr}\\
& =-\frac{1}{r}|_{k}^{2k}\\
& =\frac{1}{k}-\frac{1}{2k}\\
& =\frac{1}{2k}\mbox{ J}.
\end{alignedat}
$Salah$\begin{alignedat}{1}W & =\intop_{k}^{2k}\left(\frac{k}{r^{2}}\right)\mbox{dr}\\
& =-\frac{1}{r}|_{k}^{2k}\\
& =\frac{1}{k}-\frac{1}{2k}\\
& =\frac{1}{2k}\mbox{ J}.
\end{alignedat}
$ -
Pertanyaan ke 3 dari 5
3. Pertanyaan
Gaya yang bekerja antara dua partikel bermassa sama memenuhi fungsi jarak $F(r)=k\frac{m^{2}}{r^{2}}$. Usaha oleh gaya tersebut pada selang $r=\thicksim$ sampai $r=R$ adalah… .
Betul$\begin{alignedat}{1}W & =\intop_{\thicksim}^{R}\left(k\frac{m^{2}}{r^{2}}\right)\mbox{dr}\\
& =\left(km^{2}\right)\frac{1}{r}|_{R}^{\thicksim}\\
& =\left(km^{2}\right)\left(\frac{1}{\thicksim}-\frac{1}{R}\right)\\
& =-\frac{km^{2}}{R}\mbox{ J}.
\end{alignedat}
$Salah$\begin{alignedat}{1}W & =\intop_{\thicksim}^{R}\left(k\frac{m^{2}}{r^{2}}\right)\mbox{dr}\\
& =\left(km^{2}\right)\frac{1}{r}|_{R}^{\thicksim}\\
& =\left(km^{2}\right)\left(\frac{1}{\thicksim}-\frac{1}{R}\right)\\
& =-\frac{km^{2}}{R}\mbox{ J}.
\end{alignedat}
$ -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Gaya untuk meregangkan pegas memenuhi fungsi peregangan $F(x)=kx$ dengan $k$ adalah konstanta pegas. Usaha untuk meregangkan pegas dari $x=0$ hingga $x=d$ adalah… .
Betul$\begin{alignedat}{1}W & =\int_{0}^{d}kx\mbox{ dx}\\
& =\frac{1}{2}kx^{2}|_{0}^{d}\\
& =\frac{1}{2}kd^{2}.
\end{alignedat}
$Salah$\begin{alignedat}{1}W & =\int_{0}^{d}kx\mbox{ dx}\\
& =\frac{1}{2}kx^{2}|_{0}^{d}\\
& =\frac{1}{2}kd^{2}.
\end{alignedat}
$ -
Pertanyaan ke 5 dari 5
5. Pertanyaan
Hubungan antara gaya dan perpindahan digambarkan seperti grafik berikut.

Besar gaya sebagai fungsi perpindahan dan usaha untuk rentang $x=0$ sampai $x=20$ m berdasarkan grafik di atas adalah… .BetulBerdasarkan grafik, maka $F(x)=(5+x)\mbox{ N}.$ Sehingga
$\begin{alignedat}{1}W & =\intop_{0}^{20}\left(5+x\right)dx\\
& =(5x+\frac{1}{2}x^{2})_{0}^{20}\\
& =300\mbox{ J.}
\end{alignedat}
$SalahBerdasarkan grafik, maka $F(x)=(5+x)\mbox{ N}.$ Sehingga
$\begin{alignedat}{1}W & =\intop_{0}^{20}\left(5+x\right)dx\\
& =(5x+\frac{1}{2}x^{2})_{0}^{20}\\
& =300\mbox{ J.}
\end{alignedat}
$