Kalau kamu ingin belajar luas segitiga dengan trigonometri secara lebih mendalam, coba simak penjelasan yang ada di sini. Setelah menerima materi, kamu bisa langsung mempraktikkannya dengan mengerjakan latihan soal yang telah kami sediakan.
Di sini, kamu akan belajar tentang Luas Segitiga dengan Trigonometri melalui video yang dibawakan oleh Bapak Anton Wardaya. Kamu akan diajak untuk memahami materi hingga metode menyelesaikan soal.
Selain itu, kamu juga akan mendapatkan latihan soal interaktif dalam 3 tingkat kesulitan (mudah, sedang, sukar). Maka dari itu, kamu bisa langsung mempraktikkan materi yang didapatkan.
Sekarang, kamu bisa mulai belajar dengan 2 video dan 3 set latihan soal yang ada di halaman ini. Apabila materi ini berguna, bagikan ke teman atau rekan kamu supaya mereka juga mendapatkan manfaatnya.
Kamu dapat download modul & contoh soal serta kumpulan latihan soal lengkap dalam bentuk pdf pada list dibawah ini:
Pembuktian Luas Segitiga dengan Trigonometri
Contoh Soal Luas Segitiga dengan Trigonometri
Latihan Soal Luas Segitiga Dengan Trigonometri (Mudah)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Pada segitiga ABC, diketahui sisi $a=10$ cm, $b=20$ cm, dan sudut $C=60^{\circ}$. Luas segita ABC adalah…
BetulL segitiga $ABC=\frac{1}{2}\cdot a\cdot b\cdot sin\, A$$=\frac{1}{2}\cdot10\cdot20\cdot sin\,60^{\circ}$$=\frac{1}{2}\cdot10\cdot20\cdot\frac{1}{2}\sqrt{3}$$=50\sqrt{3}\, cm^{2}$
SalahL segitiga $ABC=\frac{1}{2}\cdot a\cdot b\cdot sin\, A$$=\frac{1}{2}\cdot10\cdot20\cdot sin\,60^{\circ}$$=\frac{1}{2}\cdot10\cdot20\cdot\frac{1}{2}\sqrt{3}$$=50\sqrt{3}\, cm^{2}$
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Luas segitiga dibawah ini adalah…
 Betul
BetulLuas segitiga $=\frac{1}{2}\cdot6\cdot8\cdot sin\,30^{\circ}$$=\frac{1}{2}\cdot6\cdot8\cdot\frac{1}{2}$$=12\, cm^{2}$
SalahLuas segitiga $=\frac{1}{2}\cdot6\cdot8\cdot sin\,30^{\circ}$$=\frac{1}{2}\cdot6\cdot8\cdot\frac{1}{2}$$=12\, cm^{2}$
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
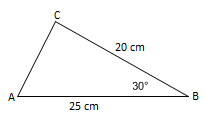
Luas segitiga $ABC$ adalah…
 Betul
Betul$L\,\triangle ABC=\frac{1}{2}\cdot AB\cdot BC$$=\frac{1}{2}\cdot25\cdot20\cdot sin\,30^{\circ}$$=\frac{1}{2}\cdot25\cdot20\cdot\frac{1}{2}$$=125\, cm^{2}$
Salah$L\,\triangle ABC=\frac{1}{2}\cdot AB\cdot BC$$=\frac{1}{2}\cdot25\cdot20\cdot sin\,30^{\circ}$$=\frac{1}{2}\cdot25\cdot20\cdot\frac{1}{2}$$=125\, cm^{2}$
-
Pertanyaan ke 4 dari 5
4. Pertanyaan
Diketahui suatu segitiga $PQR$ dengan$\angle P=150^{\circ}$, panjang sisi $q=12$ cm dan sisi $r=5$ cm. Luas segitiga $PQR$ adalah…
BetulPerahatikan gambar berikut!

$L\,\triangle PQR=\frac{1}{2}\cdot q\cdot r\cdot sin\, P$
$L\,\triangle PQR=\frac{1}{2}\cdot12\cdot5\cdot sin\,150^{\circ}$$=30\cdot sin\,(180-30)^{\circ}$$=30\cdot sin\,30^{\circ}$$=30\cdot\frac{1}{2}$$=15$
Jadi luas segitiga $PQR$ adalah $15\, cm^{2}$
SalahPerahatikan gambar berikut!

$L\,\triangle PQR=\frac{1}{2}\cdot q\cdot r\cdot sin\, P$
$L\,\triangle PQR=\frac{1}{2}\cdot12\cdot5\cdot sin\,150^{\circ}$$=30\cdot sin\,(180-30)^{\circ}$$=30\cdot sin\,30^{\circ}$$=30\cdot\frac{1}{2}$$=15$
Jadi luas segitiga $PQR$ adalah $15\, cm^{2}$
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Dari segitiga $ABC$ diketahui $a=4\, cm$, $b=3\, cm$, Jika luas segitiga $=6\, cm^{2}$ sudut $C$ adalah…
BetulLuas segitiga $ABC=\frac{1}{2}\cdot a\cdot b\cdot sin\, C$
$6=\frac{1}{2}\cdot4\cdot3\cdot sin\, C\rightarrow sin\, C=1$
Jadi $C=90^{\circ}.$
SalahLuas segitiga $ABC=\frac{1}{2}\cdot a\cdot b\cdot sin\, C$
$6=\frac{1}{2}\cdot4\cdot3\cdot sin\, C\rightarrow sin\, C=1$
Jadi $C=90^{\circ}.$
Latihan Soal Luas Segitiga Dengan Trigonometri (Sedang)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Luas segitiga sama sisi dengan panjang $8\sqrt{3}$ cm adalah…$cm^{2}$
BetulMisalkan segitiga sama sisi ABC
Semua sudut segitiga sama sisi sama besar yaitu $\angle A=\angle B=\angle C=60^{\circ}$ dan panjang ketiga sisinya sama besar yaitu $a=b=c=8\sqrt{3}$ cm
$L=\frac{1}{2}ab\, sin\, C$
$L=\frac{1}{2}\cdot8\sqrt{3}\cdot8\sqrt{3}\cdot sin\,60^{\circ}$
$L=96\cdot\frac{1}{2}\sqrt{3}=48\sqrt{3}$
SalahMisalkan segitiga sama sisi ABC
Semua sudut segitiga sama sisi sama besar yaitu $\angle A=\angle B=\angle C=60^{\circ}$ dan panjang ketiga sisinya sama besar yaitu $a=b=c=8\sqrt{3}$ cm
$L=\frac{1}{2}ab\, sin\, C$
$L=\frac{1}{2}\cdot8\sqrt{3}\cdot8\sqrt{3}\cdot sin\,60^{\circ}$
$L=96\cdot\frac{1}{2}\sqrt{3}=48\sqrt{3}$
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Diketahui segitiga $ABC$ dengan panjang sisi $AB=6$ cm, besar $\angle A=30^{\circ}$, $\angle C=120^{\circ}$, luas segitiga $ABC$ adalah…
BetulPerhatikan gambar berikut!

$\angle B=180^{\circ}-\left(\angle A+\angle C\right)$$=180^{\circ}-\left(30^{\circ}+120^{\circ}\right)=30^{\circ}$
$L=\frac{c^{2}.sin\, A\cdot sin\, B}{2\cdot sin\, C}$$=\frac{6^{2}\cdot sin\,30^{\circ}\cdot sin\,30^{\circ}}{2\cdot sin\,120^{\circ}}$$=\frac{36\cdot\frac{1}{2}\cdot\frac{1}{2}}{2.\frac{1}{2}\sqrt{3}}$$=\frac{9}{\sqrt{3}}\cdot\frac{\sqrt{3}}{\sqrt{3}}$$=3\sqrt{3}\, cm^{2}$
SalahPerhatikan gambar berikut!

$\angle B=180^{\circ}-\left(\angle A+\angle C\right)$$=180^{\circ}-\left(30^{\circ}+120^{\circ}\right)=30^{\circ}$
$L=\frac{c^{2}.sin\, A\cdot sin\, B}{2\cdot sin\, C}$$=\frac{6^{2}\cdot sin\,30^{\circ}\cdot sin\,30^{\circ}}{2\cdot sin\,120^{\circ}}$$=\frac{36\cdot\frac{1}{2}\cdot\frac{1}{2}}{2.\frac{1}{2}\sqrt{3}}$$=\frac{9}{\sqrt{3}}\cdot\frac{\sqrt{3}}{\sqrt{3}}$$=3\sqrt{3}\, cm^{2}$
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Luas segitiga ABC $35\, cm^{2}$. Jika panjang $AB=10$ cm, panjang $BC=14$ cm dan B sudut lancip maka nilai dari $cos\,(-B)$ sama dengan…
BetulPerhatikan gambar berikut!

$L=\frac{1}{2}\cdot AB\cdot BC\cdot sin\, B$
$35=\frac{1}{2}\cdot10\cdot14\cdot sin\, B$
$35=70\cdot sin\, B$
$sin\, B=\frac{35}{70}=\frac{1}{2}$
$sin\, B=sin\,30^{\circ}=sin\,150^{\circ}$
$B=\left(30^{\circ},\,150^{\circ}\right)$
Karena $B$ lancip, maka $B=30^{\circ}$
Jadi nilai $cos\,(-B)=cos\, B=cos\,30^{\circ}=\frac{1}{2}\sqrt{3}.$
SalahPerhatikan gambar berikut!

$L=\frac{1}{2}\cdot AB\cdot BC\cdot sin\, B$
$35=\frac{1}{2}\cdot10\cdot14\cdot sin\, B$
$35=70\cdot sin\, B$
$sin\, B=\frac{35}{70}=\frac{1}{2}$
$sin\, B=sin\,30^{\circ}=sin\,150^{\circ}$
$B=\left(30^{\circ},\,150^{\circ}\right)$
Karena $B$ lancip, maka $B=30^{\circ}$
Jadi nilai $cos\,(-B)=cos\, B=cos\,30^{\circ}=\frac{1}{2}\sqrt{3}.$
-
Pertanyaan ke 4 dari 5
4. Pertanyaan
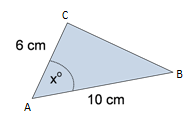
Perhatikan gambar berikut!

Jika luas segitiga ABC adalah $25\, cm^{2}$, maka nilai dari $sin\, x$ adalah…
Betul$L\,\triangle ABC=\frac{1}{2}\cdot AC\cdot AB\cdot sin\, A$
$25=\frac{1}{2}\cdot10\cdot6.sin\, x^{\circ}$
$50=60\cdot sin\, x^{\circ}$
$sin\, x^{\circ}=\frac{50}{60}=\frac{5}{6}$
Salah$L\,\triangle ABC=\frac{1}{2}\cdot AC\cdot AB\cdot sin\, A$
$25=\frac{1}{2}\cdot10\cdot6.sin\, x^{\circ}$
$50=60\cdot sin\, x^{\circ}$
$sin\, x^{\circ}=\frac{50}{60}=\frac{5}{6}$
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Diketahui segitiga ABC dengan panjang sisi $a=3$ cm, $b=6$ cm, dan $c=\sqrt{21}$ cm, luas segitiga ABC adalah…
BetulL segitiga ABC = $\frac{1}{2}a\cdot b\cdot sinc$
$cos\, C=\frac{3^{2}+6^{2}-\left(\sqrt{21}\right)^{2}}{2.3.6}$$=\frac{9+36-21}{36}$$=\frac{24}{36}$$=\frac{6}{9}$
$sin\, C=\frac{3\sqrt{5}}{9}=\frac{1}{3}\sqrt{5}$
Jadi luas segitiga ABC $=\frac{1}{2}\cdot3\cdot6\cdot\frac{1}{3}\sqrt{5}=3\sqrt{5}.$
SalahL segitiga ABC = $\frac{1}{2}a\cdot b\cdot sinc$
$cos\, C=\frac{3^{2}+6^{2}-\left(\sqrt{21}\right)^{2}}{2.3.6}$$=\frac{9+36-21}{36}$$=\frac{24}{36}$$=\frac{6}{9}$
$sin\, C=\frac{3\sqrt{5}}{9}=\frac{1}{3}\sqrt{5}$
Jadi luas segitiga ABC $=\frac{1}{2}\cdot3\cdot6\cdot\frac{1}{3}\sqrt{5}=3\sqrt{5}.$
Latihan Soal Luas Segitiga Dengan Trigonometri (Sukar)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
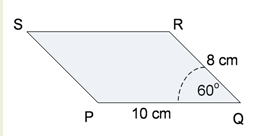
Perhatikan Jajaran genjang PQRS berikut ini!

Luas jajaran genjang PQRS adalah…
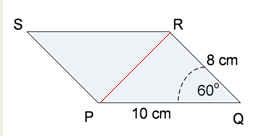
BetulPerhatikan gambar berikut!

$L\,\triangle PQR=L\triangle PSR$
$L\,\triangle PQR=\frac{1}{2}\cdot PQ\cdot QR\cdot sin\, Q$
$L\,\triangle PQR=\frac{1}{2}\cdot10\cdot8\cdot sin\,60^{\circ}$$=\frac{1}{2}\cdot10\cdot8\cdot\frac{1}{2}\sqrt{3}$$=20\sqrt{3}$ cm
$L\,\triangle PQRS=2\cdot L\triangle PQR$$=2\cdot20\sqrt{3}$$=40\sqrt{3}$
SalahPerhatikan gambar berikut!

$L\,\triangle PQR=L\triangle PSR$
$L\,\triangle PQR=\frac{1}{2}\cdot PQ\cdot QR\cdot sin\, Q$
$L\,\triangle PQR=\frac{1}{2}\cdot10\cdot8\cdot sin\,60^{\circ}$$=\frac{1}{2}\cdot10\cdot8\cdot\frac{1}{2}\sqrt{3}$$=20\sqrt{3}$ cm
$L\,\triangle PQRS=2\cdot L\triangle PQR$$=2\cdot20\sqrt{3}$$=40\sqrt{3}$
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Jajaran genjang ABCD, diketahui $AB=5$ cm, $BC=4$ cm dan $\angle ABC=120^{\circ}$, maka luas jajaran genjang itu sama dengan …$cm^{2}$
BetulLuas jajaran genjang ABCD $=2\times L\triangle ABC$
Luas jajaran genjang ABCD $=2\times\frac{1}{2}\times AB\times BC\, sin\,\angle ABC$$=2\cdot\frac{1}{2}\cdot(5)\cdot(4)\, sin\,120^{\circ}$$=20\cdot\frac{1}{2}\sqrt{3}=10\sqrt{3}$
SalahLuas jajaran genjang ABCD $=2\times L\triangle ABC$
Luas jajaran genjang ABCD $=2\times\frac{1}{2}\times AB\times BC\, sin\,\angle ABC$$=2\cdot\frac{1}{2}\cdot(5)\cdot(4)\, sin\,120^{\circ}$$=20\cdot\frac{1}{2}\sqrt{3}=10\sqrt{3}$
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Di dalam suatu lingkaran dengan jari-jari $10$ cm dibuat segi $6$ beraturan. Luas segi enam tersebut adalah…
Betul
Dari segi enam terbentuk $6$ segitiga sama sisi dengan sudut $60^{\circ}$
Luas $1$ segitiga $=\frac{1}{2}\cdot10\cdot10\cdot sin\,60^{\circ}$$=\frac{1}{2}\cdot10\cdot10\cdot\frac{1}{2}\sqrt{3}$$=25\sqrt{3}\, cm^{2}$
Luas segi $6=6\times$ luas segitiga $=6\cdot5\sqrt{3}\, cm^{2}$$=150\sqrt{3}\, cm^{2}$
Salah
Dari segi enam terbentuk $6$ segitiga sama sisi dengan sudut $60^{\circ}$
Luas $1$ segitiga $=\frac{1}{2}\cdot10\cdot10\cdot sin\,60^{\circ}$$=\frac{1}{2}\cdot10\cdot10\cdot\frac{1}{2}\sqrt{3}$$=25\sqrt{3}\, cm^{2}$
Luas segi $6=6\times$ luas segitiga $=6\cdot5\sqrt{3}\, cm^{2}$$=150\sqrt{3}\, cm^{2}$
-
Pertanyaan ke 4 dari 5
4. Pertanyaan
Pada sebuah lingkaran dibuat segi$-12$ beraturan. Jika jari-jari lingkaran adalah $10$ cm, maka luas segi$-12$ yang terbentuk adalah…
BetulUntuk menentukan luas segi$-n$ beraturan yang dibuat di dalam suatu lingkaran yang berjari-jari $r$, dasarnya dari luas segitiga menggunakan sinus, dikalikan banyaknya segitiga yang terbentuk.
$L=\frac{1}{2}nr^{2}\cdot sin\,\frac{2\pi}{n}$
$L=\frac{1}{2}\cdot12\cdot10^{2}\cdot sin\,\frac{2\pi}{12}$
$L=600\cdot sin\,30^{\circ}$$=600\cdot\frac{1}{2}=300$
Jadi luas segi$-12$ beraturan yang terbentuk adalah $300\, cm^{2}.$
SalahUntuk menentukan luas segi$-n$ beraturan yang dibuat di dalam suatu lingkaran yang berjari-jari $r$, dasarnya dari luas segitiga menggunakan sinus, dikalikan banyaknya segitiga yang terbentuk.
$L=\frac{1}{2}nr^{2}\cdot sin\,\frac{2\pi}{n}$
$L=\frac{1}{2}\cdot12\cdot10^{2}\cdot sin\,\frac{2\pi}{12}$
$L=600\cdot sin\,30^{\circ}$$=600\cdot\frac{1}{2}=300$
Jadi luas segi$-12$ beraturan yang terbentuk adalah $300\, cm^{2}.$
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Luas segitiga ABC adalah $\left(3+2\sqrt{3}\right)\, cm^{2}$. Panjang sisi $AB=\left(6+4\sqrt{3}\right)$ cm dan $BC=7$ cm. Nilai $sin\,(A+C)=…$
BetulPerhatikan gambar berikut!

$L=\frac{1}{2}\cdot AB\cdot BC\cdot sin\, B$
$\left(3+2\sqrt{3}\right)=\frac{1}{2}\cdot\left(6+4\sqrt{3}\right)\cdot7\cdot sin\, B$
$\left(3+2\sqrt{3}\right)=\left(3+2\sqrt{3}\right)\cdot7\cdot sin\, B$
$sin\, B=\frac{1}{7}$
Jumlah sudut dalam segitiga adalah $180^{\circ}$
$\angle A+\angle B+\angle C=180^{\circ}$
$\angle B=180^{\circ}-\left(\angle A+\angle C\right)$
$sin\,\angle B=sin\,\left(180^{\circ}-\left(\angle A+\angle C\right)\right)$
$sin\, B=sin\,\left(\angle A+\angle C\right)=\frac{1}{7}$
SalahPerhatikan gambar berikut!

$L=\frac{1}{2}\cdot AB\cdot BC\cdot sin\, B$
$\left(3+2\sqrt{3}\right)=\frac{1}{2}\cdot\left(6+4\sqrt{3}\right)\cdot7\cdot sin\, B$
$\left(3+2\sqrt{3}\right)=\left(3+2\sqrt{3}\right)\cdot7\cdot sin\, B$
$sin\, B=\frac{1}{7}$
Jumlah sudut dalam segitiga adalah $180^{\circ}$
$\angle A+\angle B+\angle C=180^{\circ}$
$\angle B=180^{\circ}-\left(\angle A+\angle C\right)$
$sin\,\angle B=sin\,\left(180^{\circ}-\left(\angle A+\angle C\right)\right)$
$sin\, B=sin\,\left(\angle A+\angle C\right)=\frac{1}{7}$