Luas daerah merupakan salah satu materi matematika yang cukup menarik untuk dibahas. Kalau kebetulan kamu ingin belajar tentang materi ini lebih dalam, simak penjelasan lengkapnya berikut. Kami juga telah menyediakan soal latihan yang bisa dikerjakan untuk mengasah kemampuanmu.
Di sini, kamu akan belajar tentang Luas Daerah melalui video yang dibawakan oleh Bapak Anton Wardaya. Kamu akan diajak untuk memahami materi hingga metode menyelesaikan soal.
Selain itu, kamu juga akan mendapatkan latihan soal interaktif dalam 3 tingkat kesulitan (mudah, sedang, sukar). Maka dari itu, kamu bisa langsung mempraktikkan materi yang didapatkan.
Sekarang, kamu bisa mulai belajar dengan 3 video dan 3 set latihan soal yang ada di halaman ini. Apabila materi ini berguna, bagikan ke teman atau rekan kamu supaya mereka juga mendapatkan manfaatnya.
Kamu dapat download modul & contoh soal serta kumpulan latihan soal lengkap dalam bentuk pdf pada list dibawah ini:
Luas Daerah Dibatasi oleh Satu Kurva
Luas Daerah Dibatasi oleh Dua Kurva
Contoh Soal Luas Daerah
Latihan Soal Luas Daerah (Mudah)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Luas daerah yang dibatasi oleh $y=3x$, $x=2$, dan $y=0$ adalah…satuan.
BetulPerhatikan gambar berikut :

Daerah yang diarsir merupakan daerah yang memenuhi $y=3x$, $x=2$, dan $y=0$
$\begin{aligned}L & =\int_{0}^{2}3x\, dx\\
& =\left[\frac{3}{2}x^{2}\right]_{0}^{2}\\
& =\frac{3}{2}(2)^{2}-\frac{3}{2}(0)^{2}\\
& =6-0\\
& =6
\end{aligned}
$Jadi luas daerahnya adalah $6$ satuan luas.
SalahPerhatikan gambar berikut :

Daerah yang diarsir merupakan daerah yang memenuhi $y=3x$, $x=2$, dan $y=0$
$\begin{aligned}L & =\int_{0}^{2}3x\, dx\\
& =\left[\frac{3}{2}x^{2}\right]_{0}^{2}\\
& =\frac{3}{2}(2)^{2}-\frac{3}{2}(0)^{2}\\
& =6-0\\
& =6
\end{aligned}
$Jadi luas daerahnya adalah $6$ satuan luas.
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Luas daerha dibawah kurva $y=-x^{2}+8x$ diatas garis $y=6x-24$ dan terletak dia kuadran I adalah…
BetulTitik potong antara kurva $y=-x^{2}+8x$ dan garis $y=6x-24$:
$-x^{2}+8x=6x-24$
$x^{2}-2x-24=0$
$\left(x-6\right)(x+4)=0$
$x=6$ atau $x=-4$
Perhatikan gambar berikut :

Luas D1 $=\int_{0}^{4}\left(-x^{2}+8x\right)\, dx$
Luas D2 $=\int_{6}^{8}\left(-x^{2}+2x+24\right)\, dx$
Jadi luas daerah keseluruhan$=\int_{0}^{4}\left(-x^{2}+8x\right)dx$$+\int_{4}^{8}\left(-x^{2}+2x+24\right)dx.$
SalahTitik potong antara kurva $y=-x^{2}+8x$ dan garis $y=6x-24$:
$-x^{2}+8x=6x-24$
$x^{2}-2x-24=0$
$\left(x-6\right)(x+4)=0$
$x=6$ atau $x=-4$
Perhatikan gambar berikut :

Luas D1 $=\int_{0}^{4}\left(-x^{2}+8x\right)\, dx$
Luas D2 $=\int_{6}^{8}\left(-x^{2}+2x+24\right)\, dx$
Jadi luas daerah keseluruhan$=\int_{0}^{4}\left(-x^{2}+8x\right)dx$$+\int_{4}^{8}\left(-x^{2}+2x+24\right)dx.$
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Luas daerah yang dibatasi oleh kurva $y=2\, sinx$, $x=\frac{\pi}{2}$ , $x=\frac{3\pi}{2}$ dan sumbu $x$ sama dengan…
BetulPerhatikan kurva $y=2\, sinx$

$\mbox{Luas}=\begin{array}{c}
\pi\\
\int\\
\frac{\pi}{2}
\end{array}2\sin x-\begin{array}{c}
3\frac{\pi}{2}\\
\int\\
\pi
\end{array}2\sin x$$\begin{aligned}\mbox{Luas } & =2\int_{\frac{\pi}{2}}^{\pi}2\sin x\, dx\\
& =4\left[-cosx\right]_{\frac{\pi}{2}}^{\pi}\\
& =4\left\{ -cos\pi-\left(-cos\frac{\pi}{2}\right)\right\} \\
& =4\left(1-0\right)=4
\end{aligned}
$Jadi luas derahnya adalah 4 satuan luas.
SalahPerhatikan kurva $y=2\, sinx$

$\mbox{Luas}=\begin{array}{c}
\pi\\
\int\\
\frac{\pi}{2}
\end{array}2\sin x-\begin{array}{c}
3\frac{\pi}{2}\\
\int\\
\pi
\end{array}2\sin x$$\begin{aligned}\mbox{Luas } & =2\int_{\frac{\pi}{2}}^{\pi}2\sin x\, dx\\
& =4\left[-cosx\right]_{\frac{\pi}{2}}^{\pi}\\
& =4\left\{ -cos\pi-\left(-cos\frac{\pi}{2}\right)\right\} \\
& =4\left(1-0\right)=4
\end{aligned}
$Jadi luas derahnya adalah 4 satuan luas.
-
Pertanyaan ke 4 dari 5
4. Pertanyaan
Daerah R dibatasi oleh kurva $y=x^{2}$, $y=x^{2}-4x+4$ dan $y=0$. Integral menyatakan luas daerah R adalah…
BetulTitik potong kurva $y=x^{2}$, $y=x^{2}-4x+4$
$x^{2}=x^{2}-4x+4$
$4x=4$
$x=1$
Perhatikan gambar berikut :

Luas D1 $=\int_{0}^{1}x^{2}dx$
Luas D1 $=\int_{1}^{2}\left(x^{2}-4x+4\right)\, dx$
Luas daerah keseluruhan $=\int_{0}^{1`}x^{2}dx+\int_{1}^{2}\left(x^{2}-4x+4\right)\, dx.$
SalahTitik potong kurva $y=x^{2}$, $y=x^{2}-4x+4$
$x^{2}=x^{2}-4x+4$
$4x=4$
$x=1$
Perhatikan gambar berikut :

Luas D1 $=\int_{0}^{1}x^{2}dx$
Luas D1 $=\int_{1}^{2}\left(x^{2}-4x+4\right)\, dx$
Luas daerah keseluruhan $=\int_{0}^{1`}x^{2}dx+\int_{1}^{2}\left(x^{2}-4x+4\right)\, dx.$
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Luas daerah yang dibatasi oleh garis $x-y=1$ dan kurva $y^{2}=x+1$ adalah … satuan luas.
 Betul
BetulCari titik portong kurva terlebih dahulu
$x-y=1$$\rightarrow x=y+1$ ….(1)
$x=y^{2}-1$….(2)
substitusikan pers (1) ke pers (2) sehingga diperoleh :
$y+1=y^{2}-1$
$y^{2}-y-2=0$
$\left(y-2\right)(y+1)=0$
$y=2$$\rightarrow x=2+1=3$, koordinat titik potong (3,2)
$y=-1$$\rightarrow x=-1+1=0$, koordinat titik potong (0,-1)
$L=\int_{-1}^{2}\{y+1-\left(y^{2}-1\right)\}dy$
$L=\int_{-1}^{2}(-y^{2}+y+2)dy$
$=\left[-\frac{1}{3}y^{3}+\frac{1}{2}y^{2}+2y\right]_{-1}^{2}$
$=\left(-\frac{1}{3}(2)^{3}+\frac{1}{2}(2)^{2}+2(2)\right)$$-\left(-\frac{1}{3}(-1)+\frac{1}{2}(-1)^{2}+2(-1)\right)$
$\begin{alignedat}{1}L & =-\frac{8}{3}+2+4-(\frac{1}{3}+\frac{1}{2}-2)\\
& =-\frac{9}{3}+6+2-\frac{1}{2}\\
& =4\frac{1}{2}.
\end{alignedat}
$SalahCari titik portong kurva terlebih dahulu
$x-y=1$$\rightarrow x=y+1$ ….(1)
$x=y^{2}-1$….(2)
substitusikan pers (1) ke pers (2) sehingga diperoleh :
$y+1=y^{2}-1$
$y^{2}-y-2=0$
$\left(y-2\right)(y+1)=0$
$y=2$$\rightarrow x=2+1=3$, koordinat titik potong (3,2)
$y=-1$$\rightarrow x=-1+1=0$, koordinat titik potong (0,-1)
$L=\int_{-1}^{2}\{y+1-\left(y^{2}-1\right)\}dy$
$L=\int_{-1}^{2}(-y^{2}+y+2)dy$
$=\left[-\frac{1}{3}y^{3}+\frac{1}{2}y^{2}+2y\right]_{-1}^{2}$
$=\left(-\frac{1}{3}(2)^{3}+\frac{1}{2}(2)^{2}+2(2)\right)$$-\left(-\frac{1}{3}(-1)+\frac{1}{2}(-1)^{2}+2(-1)\right)$
$\begin{alignedat}{1}L & =-\frac{8}{3}+2+4-(\frac{1}{3}+\frac{1}{2}-2)\\
& =-\frac{9}{3}+6+2-\frac{1}{2}\\
& =4\frac{1}{2}.
\end{alignedat}
$
Latihan Soal Luas Daerah (Sedang)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Luas daerah yang dibatasi oleh kurva $y=12-3x^{2}$, garis $y=6-3x$, garis $x=-1$, dan garis $x=1$ adalah…satuan luas.
BetulSketsa grafiknya seperti gambar berikut!

$L=\int_{-1}^{1}(12-3x^{2}-(6-3x))\, dx$
$=\int_{-1}^{1}(-3x^{2}+3x+6)\, dx$
$=3\int_{-1}^{1}(-x^{2}+x+2)\, dx$
$L=3\left[-\frac{1}{3}x^{3}+\frac{1}{2}x^{2}+2x\right]_{-1}^{1}$
$=3\{-\frac{1}{3}(1)^{3}+\frac{1}{2}(1)^{2}+2(1)$$-\left(-\frac{1}{3}(-1)^{3}+\frac{1}{2}(-1)^{2}+2(-1)\right)\}$
$=3\left[-\frac{1}{3}+\frac{1}{2}+2-\frac{1}{3}-\frac{1}{2}+2\right]$
$=3\left(4-\frac{2}{3}\right)$
$=3(\frac{10}{3})$
$=10$
Jadi luas daerah yang diarsir adalah $10$ satuan luas.
SalahSketsa grafiknya seperti gambar berikut!

$L=\int_{-1}^{1}(12-3x^{2}-(6-3x))\, dx$
$=\int_{-1}^{1}(-3x^{2}+3x+6)\, dx$
$=3\int_{-1}^{1}(-x^{2}+x+2)\, dx$
$L=3\left[-\frac{1}{3}x^{3}+\frac{1}{2}x^{2}+2x\right]_{-1}^{1}$
$=3\{-\frac{1}{3}(1)^{3}+\frac{1}{2}(1)^{2}+2(1)$$-\left(-\frac{1}{3}(-1)^{3}+\frac{1}{2}(-1)^{2}+2(-1)\right)\}$
$=3\left[-\frac{1}{3}+\frac{1}{2}+2-\frac{1}{3}-\frac{1}{2}+2\right]$
$=3\left(4-\frac{2}{3}\right)$
$=3(\frac{10}{3})$
$=10$
Jadi luas daerah yang diarsir adalah $10$ satuan luas.
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
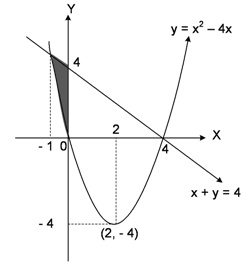
Integral yang menyatakan luas daerah yang diarsir adalah…
 Betul
BetulDaerah yang diarsir adalah daerah yang dibatasi garis $x+y=4$ dan kurva $y=x^{2}-4x$ dengan batas $x=-1$ dan $x=0$
$x+y=4$$\rightarrow y=4-x$
$\begin{aligned}L & =\int_{-1}^{0}(4-x-(x^{2}-4x))\, dx\\
& =\int_{-1}^{0}(-x^{2}+3x+4)\, dx\\
& =-\int_{0}^{-1}(-x^{2}+3x+4)\, dx\\
& =\int_{0}^{-1}(x^{2}-3x-4)\, dx.
\end{aligned}
$SalahDaerah yang diarsir adalah daerah yang dibatasi garis $x+y=4$ dan kurva $y=x^{2}-4x$ dengan batas $x=-1$ dan $x=0$
$x+y=4$$\rightarrow y=4-x$
$\begin{aligned}L & =\int_{-1}^{0}(4-x-(x^{2}-4x))\, dx\\
& =\int_{-1}^{0}(-x^{2}+3x+4)\, dx\\
& =-\int_{0}^{-1}(-x^{2}+3x+4)\, dx\\
& =\int_{0}^{-1}(x^{2}-3x-4)\, dx.
\end{aligned}
$ -
Pertanyaan ke 3 dari 5
3. Pertanyaan
Luas daerah yang dibatasi oleh kurva $y=-x^{2}+4x$, sumbu $x$, garis $x=1$ dan garis $x=3$ adalah…satuan luas.
BetulPerhatikan gambar berikut!

$\begin{aligned}L & =\int_{1}^{3}(-x^{2}+4x)\\
& =\left[-\frac{1}{3}x^{3}+2x^{2}\right]_{1}^{3}\\
& =\left(-\frac{1}{3}(3)^{3}+2(3)^{2}\right)-\left(-\frac{1}{3}(1)^{3}+2(1)^{2}\right)\\
& =-9+18+\frac{1}{3}-2\\
& =7\frac{1}{3}
\end{aligned}
$SalahPerhatikan gambar berikut!

$\begin{aligned}L & =\int_{1}^{3}(-x^{2}+4x)\\
& =\left[-\frac{1}{3}x^{3}+2x^{2}\right]_{1}^{3}\\
& =\left(-\frac{1}{3}(3)^{3}+2(3)^{2}\right)-\left(-\frac{1}{3}(1)^{3}+2(1)^{2}\right)\\
& =-9+18+\frac{1}{3}-2\\
& =7\frac{1}{3}
\end{aligned}
$ -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Perhatikan gambar berikut!

Luas daerah yang diarsir adalah…satuan luas.
BetulCari dulu persamaan garis lurus yang melalui titik $(0,\,3)$ dan $(1,\,4)$ :
$\frac{x-0}{1-0}=\frac{y-3}{4-3}$
$x=y-3$$\rightarrow y=x+3$
Partisikan untuk mencari luas daerah yang diarsir :

$L_{1}$ adalah daerah yang dibatasi oleh kurva $y=x^{2}$ dan garis $y=x+3:$
$\begin{aligned}L_{1} & =\int_{0}^{1}\left(x+3-x^{2}\right)\, dx\\
& =\left[\frac{1}{2}x^{2}+3x-\frac{1}{3}x^{3}\right]_{0}^{1}\\
& =\frac{1}{2}+3-\frac{1}{3}=\frac{19}{6}
\end{aligned}
$$L_{2}$ adalah daerah yang dibatasi oleh garis y = 4 dan kurva $y=x^{2}$
$\begin{aligned}L_{2} & =\int_{1}^{2}(4-x^{2})\, dx\\
& =\left[4x-\frac{1}{3}x^{3}\right]_{1}^{2}\\
& =\left(4(2)-\frac{1}{3}(2)^{3}\right)-\left(4(1)-\frac{1}{3}(1)^{3}\right)\\
& =8-\frac{8}{3}-4+\frac{1}{3}\\
& =4-\frac{7}{3}\\
& =\frac{5}{3}
\end{aligned}
$$\begin{aligned}L & =L_{1}+L_{2}\\
& =\frac{19}{6}+\frac{5}{3}\\
& =\frac{19+10}{6}\\
& =\frac{29}{6}
\end{aligned}
$Jadi luas daerah yang diarsir adalah $\frac{29}{6}$ satuan luas.
SalahCari dulu persamaan garis lurus yang melalui titik $(0,\,3)$ dan $(1,\,4)$ :
$\frac{x-0}{1-0}=\frac{y-3}{4-3}$
$x=y-3$$\rightarrow y=x+3$
Partisikan untuk mencari luas daerah yang diarsir :

$L_{1}$ adalah daerah yang dibatasi oleh kurva $y=x^{2}$ dan garis $y=x+3:$
$\begin{aligned}L_{1} & =\int_{0}^{1}\left(x+3-x^{2}\right)\, dx\\
& =\left[\frac{1}{2}x^{2}+3x-\frac{1}{3}x^{3}\right]_{0}^{1}\\
& =\frac{1}{2}+3-\frac{1}{3}=\frac{19}{6}
\end{aligned}
$$L_{2}$ adalah daerah yang dibatasi oleh garis y = 4 dan kurva $y=x^{2}$
$\begin{aligned}L_{2} & =\int_{1}^{2}(4-x^{2})\, dx\\
& =\left[4x-\frac{1}{3}x^{3}\right]_{1}^{2}\\
& =\left(4(2)-\frac{1}{3}(2)^{3}\right)-\left(4(1)-\frac{1}{3}(1)^{3}\right)\\
& =8-\frac{8}{3}-4+\frac{1}{3}\\
& =4-\frac{7}{3}\\
& =\frac{5}{3}
\end{aligned}
$$\begin{aligned}L & =L_{1}+L_{2}\\
& =\frac{19}{6}+\frac{5}{3}\\
& =\frac{19+10}{6}\\
& =\frac{29}{6}
\end{aligned}
$Jadi luas daerah yang diarsir adalah $\frac{29}{6}$ satuan luas.
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Luas kurva yang diarsir adalah…
 Betul
Betul$L=\int_{-2}^{2}\sqrt{x+2}dx$
$=\left[\frac{2}{3}(x+2)\sqrt{x+2}\right]_{-2}^{2}$
$=\left(\frac{2}{3}(2+2)\sqrt{2+2}-\left(\frac{2}{3}(-2+2)\sqrt{-2+2}\right)\right)$
$=\frac{16}{3}-0=5\frac{1}{3}$.
Salah$L=\int_{-2}^{2}\sqrt{x+2}dx$
$=\left[\frac{2}{3}(x+2)\sqrt{x+2}\right]_{-2}^{2}$
$=\left(\frac{2}{3}(2+2)\sqrt{2+2}-\left(\frac{2}{3}(-2+2)\sqrt{-2+2}\right)\right)$
$=\frac{16}{3}-0=5\frac{1}{3}$.
Latihan Soal Luas Daerah (Sukar)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Perhatikan gambar. Jika $\int_{0}^{b}x\cdot dx=\int_{0}^{b}x^{2}\cdot dx$ , luas daerah yang diarsir adalah…
 Betul
Betul$\int_{0}^{b}x\cdot dx=\int_{0}^{b}x^{2}\cdot dx$
$\left[\frac{1}{2}x^{2}\right]_{0}^{b}=\left[\frac{1}{3}x^{3}\right]_{0}^{b}$
$\frac{1}{2}b^{2}=\frac{1}{3}b^{3}$
$2b^{3}-3b^{2}=0$
$b^{2}\left(2b-3\right)=0$
$b=0$ atau $b=\frac{3}{2}$
Perpotongan antara garis $y=x^{2}$ dan garis $y=x:$
$x^{2}-x=0$
$x\left(x-1\right)=0$
$x=0$ atau $x=1$
Luas daerah yang diarsir adalah :
$L=\int_{1}^{\frac{3}{2}}(x^{2}-x)dx$
$=\left[\frac{1}{3}x^{3}-\frac{1}{2}x^{2}\right]_{1}^{\frac{3}{2}}$
$=\left(\frac{1}{3}\left(\frac{3}{2}\right)^{3}-\frac{1}{2}\left(\frac{3}{2}\right)^{2}\right)-\left(\frac{1}{3}\left(1\right)^{3}-\frac{1}{2}\left(1\right)^{2}\right)$
$=\frac{9}{8}-\frac{9}{8}-\frac{1}{3}+\frac{1}{2}$
$=\frac{1}{6}.$
Salah$\int_{0}^{b}x\cdot dx=\int_{0}^{b}x^{2}\cdot dx$
$\left[\frac{1}{2}x^{2}\right]_{0}^{b}=\left[\frac{1}{3}x^{3}\right]_{0}^{b}$
$\frac{1}{2}b^{2}=\frac{1}{3}b^{3}$
$2b^{3}-3b^{2}=0$
$b^{2}\left(2b-3\right)=0$
$b=0$ atau $b=\frac{3}{2}$
Perpotongan antara garis $y=x^{2}$ dan garis $y=x:$
$x^{2}-x=0$
$x\left(x-1\right)=0$
$x=0$ atau $x=1$
Luas daerah yang diarsir adalah :
$L=\int_{1}^{\frac{3}{2}}(x^{2}-x)dx$
$=\left[\frac{1}{3}x^{3}-\frac{1}{2}x^{2}\right]_{1}^{\frac{3}{2}}$
$=\left(\frac{1}{3}\left(\frac{3}{2}\right)^{3}-\frac{1}{2}\left(\frac{3}{2}\right)^{2}\right)-\left(\frac{1}{3}\left(1\right)^{3}-\frac{1}{2}\left(1\right)^{2}\right)$
$=\frac{9}{8}-\frac{9}{8}-\frac{1}{3}+\frac{1}{2}$
$=\frac{1}{6}.$
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Jika luas daerah yang dibatasi oleh kurva $y=\sqrt{px}$ dan garis $y=x$ adalah $\frac{3}{2}$ , maka nilai $p$ adalah…
BetulCari titik potong antara garis $y=\sqrt{px}$ dan $y=x:$
$\sqrt{px}=x$
$px=x^{2}$
$x\left(x-p\right)=0$
$x=0$ atau $x=p$
Perhatikan gambar berikut!

$\begin{aligned}L & =\int_{0}^{p}\left(\sqrt{px}-x\right)dx\\
& =\left[\frac{2}{3p}\left(px\right)^{\frac{3}{2}}-\frac{1}{2}x^{2}\right]_{0}^{p}
\end{aligned}
$$\frac{3}{2}=\frac{2}{3p}\left(p^{2}\right)^{\frac{3}{2}}-\frac{1}{2}p^{2}$
$\frac{2}{3}=\frac{2}{3}p^{2}-\frac{1}{2}p^{2}=\frac{p^{2}}{6}$
$p^{2}=4$
$p=\pm2$
$p=-2$ (tidak memenuhi) karena $px>0$
$p=2$ (memenuhi)
Jadi nilai $p$ adalah $p=2.$
SalahCari titik potong antara garis $y=\sqrt{px}$ dan $y=x:$
$\sqrt{px}=x$
$px=x^{2}$
$x\left(x-p\right)=0$
$x=0$ atau $x=p$
Perhatikan gambar berikut!

$\begin{aligned}L & =\int_{0}^{p}\left(\sqrt{px}-x\right)dx\\
& =\left[\frac{2}{3p}\left(px\right)^{\frac{3}{2}}-\frac{1}{2}x^{2}\right]_{0}^{p}
\end{aligned}
$$\frac{3}{2}=\frac{2}{3p}\left(p^{2}\right)^{\frac{3}{2}}-\frac{1}{2}p^{2}$
$\frac{2}{3}=\frac{2}{3}p^{2}-\frac{1}{2}p^{2}=\frac{p^{2}}{6}$
$p^{2}=4$
$p=\pm2$
$p=-2$ (tidak memenuhi) karena $px>0$
$p=2$ (memenuhi)
Jadi nilai $p$ adalah $p=2.$
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Daerah $D_{1}$ dibatasi oleh parabola $y=x^{2}$, garis $y=4$ dan garis $x=c$. Daerah $D_{2}$ dibatasi oleh parabola $y=x^{2}$, garis $x=c$ dan sumbu $x$. Jika luas $D_{1}$ sama dengan luas $D_{2}$, luas daerah yang diarsir adalah…
 Betul
BetulPerhatikan gambar berikut
Luas $D_{1}=$ Luas $D_{1}$
$\int_{0}^{c}(4-x^{2})dx=\int_{0}^{c}x^{2}dx$
$\left[4x-\frac{1}{3}x^{3}\right]_{c}^{2}=\left[\frac{1}{3}x^{3}\right]_{0}^{c}$
$\left(8-\frac{8}{3}\right)-\left(4c-\frac{1}{3}c^{3}\right)=\frac{1}{3}c^{3}$ (semua ruas kalikan dengan 3 )
$24-8-12c+c^{3}=c^{3}$
$12c=16$
$c=\frac{16}{12}=\frac{4}{3}$
Luas daerah yang diarsir $=4c$$=4\left(\frac{4}{3}\right)$$=\frac{16}{3}.$
SalahPerhatikan gambar berikut
Luas $D_{1}=$ Luas $D_{1}$
$\int_{0}^{c}(4-x^{2})dx=\int_{0}^{c}x^{2}dx$
$\left[4x-\frac{1}{3}x^{3}\right]_{c}^{2}=\left[\frac{1}{3}x^{3}\right]_{0}^{c}$
$\left(8-\frac{8}{3}\right)-\left(4c-\frac{1}{3}c^{3}\right)=\frac{1}{3}c^{3}$ (semua ruas kalikan dengan 3 )
$24-8-12c+c^{3}=c^{3}$
$12c=16$
$c=\frac{16}{12}=\frac{4}{3}$
Luas daerah yang diarsir $=4c$$=4\left(\frac{4}{3}\right)$$=\frac{16}{3}.$
-
Pertanyaan ke 4 dari 5
4. Pertanyaan
Jika D adalah daerah dikuadran $1$ yang dibatasi oleh parabola $y^{2}=2x$ dan garis $x-y=4$. Maka luas D adalah…
Betul$x-y=4$$\rightarrow x=y+4$…. (1)
$y^{2}=2x$ ….(2)
Cari titik perpotongan dengan mensubstitusikan pers (1) ke pers (2) :
$y^{2}=2(y+4)$
$y^{2}-2y-8=0$
$\left(y-4\right)(y+2)=0$
$y=4$, maka $x=4+4=8$
Perhatikan gambar berikut!

Luas daerah yang diarsir $=\int_{0}^{8}\sqrt{2x}dx-\int_{4}^{8}\left(x-4\right)dx$
Luas daerah yang diarsir $=\left[\frac{2x\sqrt{2x}}{3}\right]_{0}^{8}-\left[\frac{1}{2}x^{2}-4x\right]_{4}^{8}$
$=\left(\frac{16\sqrt{16}}{3}\right)-\left[\left(32-32\right)-\left(8-16\right)\right]$
$=\frac{64}{3}-8$
$=\frac{64-24}{3}$
$=\frac{40}{3}=13\frac{1}{3}.$
Salah$x-y=4$$\rightarrow x=y+4$…. (1)
$y^{2}=2x$ ….(2)
Cari titik perpotongan dengan mensubstitusikan pers (1) ke pers (2) :
$y^{2}=2(y+4)$
$y^{2}-2y-8=0$
$\left(y-4\right)(y+2)=0$
$y=4$, maka $x=4+4=8$
Perhatikan gambar berikut!

Luas daerah yang diarsir $=\int_{0}^{8}\sqrt{2x}dx-\int_{4}^{8}\left(x-4\right)dx$
Luas daerah yang diarsir $=\left[\frac{2x\sqrt{2x}}{3}\right]_{0}^{8}-\left[\frac{1}{2}x^{2}-4x\right]_{4}^{8}$
$=\left(\frac{16\sqrt{16}}{3}\right)-\left[\left(32-32\right)-\left(8-16\right)\right]$
$=\frac{64}{3}-8$
$=\frac{64-24}{3}$
$=\frac{40}{3}=13\frac{1}{3}.$
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Perhatikan gambar berikut!

Luas daerah yang diarsir adalah…
BetulCari dulu persamaan kurva.
persamaan kurva yang memotong sumbu x di titik $(-2,\,0)$ dan $(2,\,0)$ :
$y=a(x-2)\,(x+2)$
melalui titik $(0,\,-4):$
$-4=a(0-2)\,(0+2)$
$-4=-4a$$\rightarrow a=1$
$y=1(x-2)(x+2)=x^{2}-4$
Jadi persamaan kurva adalah $y=x^{2}-4$
Cari dulu persamaan garis
Persamaan garis yang melalui titik $(-1,\,-3)$ dan $(3,\,5):$
$\frac{x-(-1)}{3-(-1)}=\frac{y-(-3)}{5-(-3)}$
$\frac{x+1}{4}=\frac{y+3}{8}$
$8(x+1)=4(y+3)$
$8x+8=4y+12$$\rightarrow2x+2=y+3$
$y=2x-1$
Titik potong terhadap sumbu $x$ yaitu $\left(\frac{1}{2},\,0\right)$
Perhatikan gambar berikut :

Luas daerah yang diarsir = Luas$\triangle ABC-$ Luas $D_{1}$
Luas daerah yang diarsir
$\begin{aligned}L & =\frac{1}{2}\cdot\left(3-\frac{1}{2}\right)\cdot5-\int_{2}^{3}(x^{2}-4)dx\\
& =\frac{1}{2}\cdot\frac{5}{2}\cdot5-\left[\frac{1}{3}x^{3}-4x\right]_{2}^{3}
\end{aligned}
$Luas daerah yang diarsir
$\begin{aligned}L & =\frac{25}{4}-\left\{ \left(9-12\right)-\left(\frac{8}{3}-8\right)\right\} \\
& =\frac{25}{4}-\left(-3+8-\frac{8}{3}\right)\\
& =\frac{25}{4}+\frac{8}{3}-5\\
& =\frac{75+32-60}{12}\\
& =\frac{47}{12}.
\end{aligned}
$SalahCari dulu persamaan kurva.
persamaan kurva yang memotong sumbu x di titik $(-2,\,0)$ dan $(2,\,0)$ :
$y=a(x-2)\,(x+2)$
melalui titik $(0,\,-4):$
$-4=a(0-2)\,(0+2)$
$-4=-4a$$\rightarrow a=1$
$y=1(x-2)(x+2)=x^{2}-4$
Jadi persamaan kurva adalah $y=x^{2}-4$
Cari dulu persamaan garis
Persamaan garis yang melalui titik $(-1,\,-3)$ dan $(3,\,5):$
$\frac{x-(-1)}{3-(-1)}=\frac{y-(-3)}{5-(-3)}$
$\frac{x+1}{4}=\frac{y+3}{8}$
$8(x+1)=4(y+3)$
$8x+8=4y+12$$\rightarrow2x+2=y+3$
$y=2x-1$
Titik potong terhadap sumbu $x$ yaitu $\left(\frac{1}{2},\,0\right)$
Perhatikan gambar berikut :

Luas daerah yang diarsir = Luas$\triangle ABC-$ Luas $D_{1}$
Luas daerah yang diarsir
$\begin{aligned}L & =\frac{1}{2}\cdot\left(3-\frac{1}{2}\right)\cdot5-\int_{2}^{3}(x^{2}-4)dx\\
& =\frac{1}{2}\cdot\frac{5}{2}\cdot5-\left[\frac{1}{3}x^{3}-4x\right]_{2}^{3}
\end{aligned}
$Luas daerah yang diarsir
$\begin{aligned}L & =\frac{25}{4}-\left\{ \left(9-12\right)-\left(\frac{8}{3}-8\right)\right\} \\
& =\frac{25}{4}-\left(-3+8-\frac{8}{3}\right)\\
& =\frac{25}{4}+\frac{8}{3}-5\\
& =\frac{75+32-60}{12}\\
& =\frac{47}{12}.
\end{aligned}
$