Aplikasi program linear merupakan salah satu materi matematika yang cukup menarik untuk dibahas. Kalau kebetulan kamu ingin belajar tentang materi ini lebih dalam, simak penjelasan lengkapnya berikut. Kami juga telah menyediakan soal latihan yang bisa dikerjakan untuk mengasah kemampuanmu.
Di sini, kamu akan belajar tentang Aplikasi Program Linear melalui video yang dibawakan oleh Bapak Anton Wardaya. Kamu akan diajak untuk memahami materi hingga metode menyelesaikan soal.
Selain itu, kamu juga akan mendapatkan latihan soal interaktif dalam 3 tingkat kesulitan (mudah, sedang, sukar). Tentunya menarik, bukan? Penjelasan yang didapatkan bisa dipraktikkan secara langsung.
Sekarang, kamu bisa mulai belajar dengan 2 video dan 3 set latihan soal yang ada di halaman ini. Apabila materi ini berguna, bagikan ke teman atau rekan kamu supaya mereka juga mendapatkan manfaatnya.
Kamu dapat download modul & contoh soal serta kumpulan latihan soal lengkap dalam bentuk pdf pada list dibawah ini:
Contoh Soal Aplikasi Program Linear (1)
Contoh Soal Aplikasi Program Linear (2)
Latihan Soal Aplikasi Program Linear (Mudah)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Suatu tempat parkir seluas $200$ m$^{2}$tidak dapat menampung lebih dari $12$ mobil dan bus. Untuk memarkir sebuah mobil rata-rata diperlukan tempat seluas $10$ m$^{2}$dan untuk bus rata-rata $20$ m$^{2}.$ Jika tarif parkir motor Rp $7.000\mbox{/hari}$ dan tarif mobil Rp $15.000\mbox{/hari}$. Agar Keuntungan maksimum banyaknya bus yang harus diparkir adalah…
BetulMisalkan banyaknya mobil = x dan banyaknya bus = y

$10x+20y\leq200$$\Rightarrow x+2y\leq20$
$x+y\leq12$
$x\geq0;\, y\geq0$
$F(x,y)=7.000x+15.000y$
Perhatikan gambar dibawah ini!

Darah yang diarsir adalah darah yang memenuhi pertidaksamaan.
$F(x,y)=7.000x+15.000y$
$F(12,0)=7.000(12)+15.000(0)=84.000$
$F(0,10)=7.000(0)+15.000(10)=150.000$
$F(4,8)=7.000(4)+15.000(8)$$=28.000+120.000=148.000$
Jadi keuntungan maximum yang diperoleh tukang parkir yaitu ketika banyaknya bus yang diparkir adalah $10.$
SalahMisalkan banyaknya mobil = x dan banyaknya bus = y

$10x+20y\leq200$$\Rightarrow x+2y\leq20$
$x+y\leq12$
$x\geq0;\, y\geq0$
$F(x,y)=7.000x+15.000y$
Perhatikan gambar dibawah ini!

Darah yang diarsir adalah darah yang memenuhi pertidaksamaan.
$F(x,y)=7.000x+15.000y$
$F(12,0)=7.000(12)+15.000(0)=84.000$
$F(0,10)=7.000(0)+15.000(10)=150.000$
$F(4,8)=7.000(4)+15.000(8)$$=28.000+120.000=148.000$
Jadi keuntungan maximum yang diperoleh tukang parkir yaitu ketika banyaknya bus yang diparkir adalah $10.$
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Seorang anak diharuskan makan dua jenis tablet setiap hari. Tablet pertama mengandung $5$ unit vitamin A dan $3$ unit vitamin B, sedangkan tablet vitamin kedua mengandung $10$ unit vitamin A dan $1$ unit vitamin B. dalam suatu hari anak itu memerlukan $20$ unit vitamin A dan $5$ unit vitamin B. Jika harga tablet pertama $\$4$/biji dan tablet kedua $\$8$/biji, pengeluaran minimum untuk pembelian tablet per hari adalah…
BetulMisalkan x = banyaknya tablet I
y = banyaknya tablet II

Model pertidaksamaan yang memenuhi adalah :
$5x+10y\geq20$$\Rightarrow x+2y\geq4$
$3x+y\ge5$
$x\ge0;\, y\ge0$
$F(x,y)=4x+8y$
Perhatikan gambar dibawah ini!

Daerah yang diarsir adalah daerah yang memenuhi pertidaksamaan.
$F(x,y)=4x+8y$
$F(4,0)=4(4)+8(0)=16$ (minimum)
$F(\frac{6}{5},\frac{7}{5})=4\left(\frac{6}{5}\right)+8\left(\frac{7}{5}\right)=\frac{80}{5}=16$
$F(0,5)=4(0)+8(5)=40$ (maksimum)
Jadi pengeluaran minimumnya adalah $\$16.$
SalahMisalkan x = banyaknya tablet I
y = banyaknya tablet II

Model pertidaksamaan yang memenuhi adalah :
$5x+10y\geq20$$\Rightarrow x+2y\geq4$
$3x+y\ge5$
$x\ge0;\, y\ge0$
$F(x,y)=4x+8y$
Perhatikan gambar dibawah ini!

Daerah yang diarsir adalah daerah yang memenuhi pertidaksamaan.
$F(x,y)=4x+8y$
$F(4,0)=4(4)+8(0)=16$ (minimum)
$F(\frac{6}{5},\frac{7}{5})=4\left(\frac{6}{5}\right)+8\left(\frac{7}{5}\right)=\frac{80}{5}=16$
$F(0,5)=4(0)+8(5)=40$ (maksimum)
Jadi pengeluaran minimumnya adalah $\$16.$
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Pesawat penumpang mempunyai tempat duduk $48$ kursi. Setiap penumpang kelas utama boleh membawa bagasi $60$ kg, sedangkan kelas ekonomi $20$ kg. pesawat hanya dapat membawa bagasi $1440$ kg. Harga tiket kelas utama Rp. $150.000,-$ dan kelas ekonomi Rp. $100.000,-$. Supaya pendapatan dari penjualan tiket pada saat pesawat penuh, jumlah tempat duduk kelas utama adalah…
BetulMisalkan x = banyaknya penumpang kelas eksekutif
y = banyaknya penumpang kelas ekonomi

Pertidaksamaan yang memenuhi adalah :
$x+y\leq48$
$60x+20y\leq1.440\Rightarrow3x+y\leq72$
$x\geq0;\, y\geq0$
$F(x,y)=150.000x+100.000y$
Perhatikan gambar dibawah ini!
Daerah yang diarsir adalah daerah yang memenuhi pertidaksamaan.

Perpotongan garis $3x+y=72$ dan garis $x+y=48$ adalah $(12,36)$
Titik ujung penyelesaian ujikan ke fungsi sasaran $F(x,y)$
$F(x,y)=150.000x+100.00y$
$F(24,0)=150.000(24)+100.00(0)=3.600.000$ (minimum)
$F(12,36)=150.000(24)+100.00(36)=7.200.000$ (maksimum)
$F(0,48)=150.000(0)+100.00(48)=4.800.000$
Hasil penjualan maksimum terjadi di titik $(12,36)$ Jadi jumlah duduk kelas utama adalah $x=12.$
SalahMisalkan x = banyaknya penumpang kelas eksekutif
y = banyaknya penumpang kelas ekonomi

Pertidaksamaan yang memenuhi adalah :
$x+y\leq48$
$60x+20y\leq1.440\Rightarrow3x+y\leq72$
$x\geq0;\, y\geq0$
$F(x,y)=150.000x+100.000y$
Perhatikan gambar dibawah ini!
Daerah yang diarsir adalah daerah yang memenuhi pertidaksamaan.

Perpotongan garis $3x+y=72$ dan garis $x+y=48$ adalah $(12,36)$
Titik ujung penyelesaian ujikan ke fungsi sasaran $F(x,y)$
$F(x,y)=150.000x+100.00y$
$F(24,0)=150.000(24)+100.00(0)=3.600.000$ (minimum)
$F(12,36)=150.000(24)+100.00(36)=7.200.000$ (maksimum)
$F(0,48)=150.000(0)+100.00(48)=4.800.000$
Hasil penjualan maksimum terjadi di titik $(12,36)$ Jadi jumlah duduk kelas utama adalah $x=12.$
-
Pertanyaan ke 4 dari 5
4. Pertanyaan
Seorang ahli gizi sedang merencanakan dua buah menu A dan B. setiap gram dari menu A mengandung 1 unit karbohidrat dan 4 unit protein. Setiap gram dari menu B mengandung 3 unit karbohidrat dan 3 unit protein. Ahli gizi tersebut ingin menyiapkan menu yang mengandung setidaknya 12 unit karbohidrat dan 24 unit protein dari menu A dan B. dengan memisalkan X adalah banyaknya gram menu A dan Y adalah banyaknya gram menu B yang dibuat. Jika biaya yang diperlukan untuk membuat menu A adalah Rp 50.000,00 dan menu B Rp 75.000,00. Modal minimal yang harus dikeluarkan oleh ahli gizi terebut adalah…
Betul
Bentuk Pertidaksamaan :
$x+3y\ge12$
$4x+3y\ge24$
$x\ge0;y\ge0$
$F(x,y)=50.000x+75.000y$
Perhatikan gambar dibawah ini!

Daerah yang diarsir adalah daerah yang memenuhi pertidaksamaan.
Perpotongan antara garis $x+3y=12$ dan garis $4x+3y=24$ adalah $\left(4,\frac{8}{3}\right)$
Titik-titik ujung penyelesaian adalah $(0,8),\,\left(4,\frac{8}{3}\right),\,(12,0)$
$F(x,y)=50.000x+75.000y$
$F(0,8)=50.000(0)+75.000(8)=600.000$
$F\left(4,\frac{8}{3}\right)=50.000(4)+75.000\left(\frac{8}{3}\right)$$=200.000+200.000=400.000$ (minimum)
$F(12,0)=50.000(12)+75.000(0)=600.000$ (maksimum)
Jadi biaya minimum yang diperlukan adalah Rp. $600.000,00.$
Salah
Bentuk Pertidaksamaan :
$x+3y\ge12$
$4x+3y\ge24$
$x\ge0;y\ge0$
$F(x,y)=50.000x+75.000y$
Perhatikan gambar dibawah ini!

Daerah yang diarsir adalah daerah yang memenuhi pertidaksamaan.
Perpotongan antara garis $x+3y=12$ dan garis $4x+3y=24$ adalah $\left(4,\frac{8}{3}\right)$
Titik-titik ujung penyelesaian adalah $(0,8),\,\left(4,\frac{8}{3}\right),\,(12,0)$
$F(x,y)=50.000x+75.000y$
$F(0,8)=50.000(0)+75.000(8)=600.000$
$F\left(4,\frac{8}{3}\right)=50.000(4)+75.000\left(\frac{8}{3}\right)$$=200.000+200.000=400.000$ (minimum)
$F(12,0)=50.000(12)+75.000(0)=600.000$ (maksimum)
Jadi biaya minimum yang diperlukan adalah Rp. $600.000,00.$
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Seorang pedagang furnitur ingin mengirim barang dagangannya yang terdiri atas 1.200 kursi dan 400 meja. Untuk keperluan tersebut, ia akan menyewa truk dan colt. Truk dapat memuat 30 kursi lipat dan 20 meja lipat, sedangkan colt dapat memuat 40 kursi lipat dan 10 meja lipat. Ongkos sewa sebuah truk Rp 200.000,00 sedangkan ongkos sewa sebuah colt Rp 160.000,00. Jumlah truk dan colt yang harus disewa agar ongkos pengiriman minimum berturut turut adalah…
BetulAgar ongkos kirim minimum, maka fungsi tujuannya adalah ongkos sewa.
Misal truk = x dan colt = y, maka fungsi tujuannya menjadi : F(x,y) = 200.000x + 160.000y

Model matematika yang memenuhi soal di atas adalah sebagai berikut :
30x + 40y $\geq$1.200$\Rightarrow$ 3x + 4y $\geq120$
20x + 10y $\geq$ 400 $\Rightarrow$ 2x + y $\geq$ 40
x$\geq0$ ; 0 y $\geq$ 0
Perhatikan gambar berikut !

Titik A,B, dan C adalah titik ujung penyelesaian.
Titik C adalah titik potong antara garis $2x+y=40$ dan garis $3x+4y=120$ yaitu $B(8,24)$
$F(x,y)=200.000x+160.000y$
$F(A)=F(0,40)=200.000(0)+160.000(40)=6.400.000$
$F(B)=F(8,24)=200.000(8)+160.000(24)=5.440.000$
$F(C)=F(40,0)=200.000(40)+160.000(0)=8.000.000$
Nilai minimumnya adalah Rp. $5.440.000,00$
Jadi yang menyebabkan nilai minimum adalah 8 truk dan 24 colt.
SalahAgar ongkos kirim minimum, maka fungsi tujuannya adalah ongkos sewa.
Misal truk = x dan colt = y, maka fungsi tujuannya menjadi : F(x,y) = 200.000x + 160.000y

Model matematika yang memenuhi soal di atas adalah sebagai berikut :
30x + 40y $\geq$1.200$\Rightarrow$ 3x + 4y $\geq120$
20x + 10y $\geq$ 400 $\Rightarrow$ 2x + y $\geq$ 40
x$\geq0$ ; 0 y $\geq$ 0
Perhatikan gambar berikut !

Titik A,B, dan C adalah titik ujung penyelesaian.
Titik C adalah titik potong antara garis $2x+y=40$ dan garis $3x+4y=120$ yaitu $B(8,24)$
$F(x,y)=200.000x+160.000y$
$F(A)=F(0,40)=200.000(0)+160.000(40)=6.400.000$
$F(B)=F(8,24)=200.000(8)+160.000(24)=5.440.000$
$F(C)=F(40,0)=200.000(40)+160.000(0)=8.000.000$
Nilai minimumnya adalah Rp. $5.440.000,00$
Jadi yang menyebabkan nilai minimum adalah 8 truk dan 24 colt.
Latihan Soal Aplikasi Program Linear (Sedang)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Tanah seluas 10.000 m² akan dibangun rumah tipe A dan tipe B. Untuk rumah tipe A diperlukan 100 m² dan tipe B diperlukan 75 m². Jumlah rumah yang dibangun paling banyak 125 unit. Keuntungan rumah tipe A adalah Rp 6.000.000,00/unit dan tipe B adalah Rp 4.000.000,00/unit. Keuntungan maksimum yang dapat diperoleh dari penjualan rumah tersebut adalah…
BetulMisalkan x = rumah tipe A dan y = rumah tipe B. Model matematika yang memenuhi adalah :
$100x+75y\le10.000\Rightarrow4x+3y\le400$
$x+y\le125$
$F(x,y)=6.000.000x+4.000.000y$
Perhatikan gambar dibawah ini!

Titik potong antara garis $4x+3y=400$ dan garis $x+y=125$ adalah $(25,100)$
Titik-titik ujung penyelesaian adalah $(0,125),(100,0)$ dan $(25,100)$
$F(x,y)=6.000.000x+4.000.000y$
$F(0,125)=6.000.000(0)+4.000.000(125)$$=500.000.000$
$F(25,100)=6.000.000(25)+4.000.000(100)$$=550.000.000$
$F(100,0)=6.000.000(100)=600.000.000$
Jadi keuntungan maksimum dari penjualan rumah adalah Rp $600.000.000,00.$
SalahMisalkan x = rumah tipe A dan y = rumah tipe B. Model matematika yang memenuhi adalah :
$100x+75y\le10.000\Rightarrow4x+3y\le400$
$x+y\le125$
$F(x,y)=6.000.000x+4.000.000y$
Perhatikan gambar dibawah ini!

Titik potong antara garis $4x+3y=400$ dan garis $x+y=125$ adalah $(25,100)$
Titik-titik ujung penyelesaian adalah $(0,125),(100,0)$ dan $(25,100)$
$F(x,y)=6.000.000x+4.000.000y$
$F(0,125)=6.000.000(0)+4.000.000(125)$$=500.000.000$
$F(25,100)=6.000.000(25)+4.000.000(100)$$=550.000.000$
$F(100,0)=6.000.000(100)=600.000.000$
Jadi keuntungan maksimum dari penjualan rumah adalah Rp $600.000.000,00.$
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Rokok A seharga Rp 200,00/bungkus dijual dengan laba Rp 40,00/bungkus sedangkan rokok B seharga Rp 100,00/bungkus dijual dengan laba Rp 30,00/bungkus.seorang pedagang rokok mempunyai modal Rp. 80.000,00 dan kios hanya mampu menampung 500 bungkus rokok. Ia akan mendapat keuntungan jika membeli…
BetulMisalkan banyaknya rokok A = x dan rokok B = y
Model matematika yang memenuhi pertidaksamaan adalah :
$x+y\leq500$
$200x+100y\leq80.000\rightarrow2x+y\leq800$
$F(x,y)=40x+30y$
Perhatikan gambar dibawah ini!

Titik potong antara garis $x+y=500$ dan garis $2x+y=800$ adalah $(300,200)$
Titik titik ujung penyelesaian adalah $(400,0),\,(300,200),\,(0,500)$
$F(x,y)=40x+30y$
$F(400,0)=40(400)+30(0)=16.000$
$F(300,200)=40(300)+30(200)=18.000$ (maksimum)
$F(0,500)=40(0)+30(500)=15.000$
Jadi keuntungan maksiimum akan diperoleh jika membeli 300 rokok A dan 200 rokok B.
SalahMisalkan banyaknya rokok A = x dan rokok B = y
Model matematika yang memenuhi pertidaksamaan adalah :
$x+y\leq500$
$200x+100y\leq80.000\rightarrow2x+y\leq800$
$F(x,y)=40x+30y$
Perhatikan gambar dibawah ini!

Titik potong antara garis $x+y=500$ dan garis $2x+y=800$ adalah $(300,200)$
Titik titik ujung penyelesaian adalah $(400,0),\,(300,200),\,(0,500)$
$F(x,y)=40x+30y$
$F(400,0)=40(400)+30(0)=16.000$
$F(300,200)=40(300)+30(200)=18.000$ (maksimum)
$F(0,500)=40(0)+30(500)=15.000$
Jadi keuntungan maksiimum akan diperoleh jika membeli 300 rokok A dan 200 rokok B.
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Suatu perusahaan meubel memerlukan 18 unsur A dan 24 unsur B per hari. Untuk membuat barang jenis I dibutuhkan 1 unsur A dan 2 unsur B, sedangkan untuk membuat barang jenis II dibutuhkan 3 unsur A dan 2 unsur B. Jika barang jenis I dijual seharga Rp 250.000,00 per unit dan barang jenis II dijual seharga Rp 400.000,00 per unit, maka agar penjualannya mencapai maksimum, banyak masing-masing barang harus dibuat adalah…
BetulMisalkan Barang I akan dibuat sebanyak x unit dan Barang II akan dibuat sebanyak y unit

Model matematika yang memenuhi adalah :
$x+3y\le18$
$2x+2y\le24\rightarrow x+y=12$
Fungsi objektifnya: $f(x,y)=250000x+400000y$
Perhatikan gambar dibawah ini!

Titik potong antara garis $2x+2y=24$ dan garis $x+3y=18$ adalah $(9,3)$
Uji Titik ujung penyelesaian ke $f(x,y)=250000x+400000$
$f(0,0)=250000(0)+400000(0)=0$
$f(12,0)=250000(12)+400000(0)$$=3.000.000$
$f(9,3)f(x,y)=250000(9)+400000(3)$$=3.450.000$ (maksimum)
$f(0,6)=250000(0)+400000(6)$$=2.400.000$
Jadi nilai maksimum terjadi jika x = 9 dan y = 3 atau dibuat 9 barang jenis I dan 3 barang jenis II.
SalahMisalkan Barang I akan dibuat sebanyak x unit dan Barang II akan dibuat sebanyak y unit

Model matematika yang memenuhi adalah :
$x+3y\le18$
$2x+2y\le24\rightarrow x+y=12$
Fungsi objektifnya: $f(x,y)=250000x+400000y$
Perhatikan gambar dibawah ini!

Titik potong antara garis $2x+2y=24$ dan garis $x+3y=18$ adalah $(9,3)$
Uji Titik ujung penyelesaian ke $f(x,y)=250000x+400000$
$f(0,0)=250000(0)+400000(0)=0$
$f(12,0)=250000(12)+400000(0)$$=3.000.000$
$f(9,3)f(x,y)=250000(9)+400000(3)$$=3.450.000$ (maksimum)
$f(0,6)=250000(0)+400000(6)$$=2.400.000$
Jadi nilai maksimum terjadi jika x = 9 dan y = 3 atau dibuat 9 barang jenis I dan 3 barang jenis II.
-
Pertanyaan ke 4 dari 5
4. Pertanyaan
Luas daerah parkir 1.760 m$^{2}$. Luas rata-rata untuk mobil kecil 4 m$^{2}$ dan mobil besar 20 m$^{2}$. Daya tampung maksimum hanya 200 kendaraan. Biaya parkir mobil kecil Rp 1.000,00/jam dan mobil besar Rp 2.000,00/jam. Jika dalam satu jam terisi penuh dan tidak ada kendaraan pergi dan datang, maka hasil maksimum tempat parkir itu adalah…
BetulMisalkan mobil kecil sebagai x, mobil besar sebagai y.
Luas parkir $1760$ m$^{2}$ $:4x+20y\le1760$ $\rightarrow x+5y\le440$……(Garis I)
Daya tampung lahan parkir 200 kendaraan: $x+y\le200$ ………(Garis II)
Fungsi objektifnya adalah hasil parkiran: $f(x,y)=1000x+2000y$
Perhatikan gambar dibawah ini!

Titik potong antara garis $x+y=200$ dan garis $x+5y=440$ adalah $(140,60)$
Titik ujung penyelesaian yaitu $(0,0),\,(200,0),\,(140,60),\,(0,88)$
Masukkan koordinat titik-titik uji / warna merah ke $f(x,y)=1000x+2000y.$
$f(0,0)=1000(0)+200(0)=0$
$f(200,0)=1000(200)+2000(0)$$=200.000$
$f(0,88)=1000(0)+2000(88)$$=176.000$
$f(140,60)=1000(140)+2000(60)=260.000$ (maksimum)
Jadi hasil parkiran maksimum adalah Rp. $260.000,00.$
SalahMisalkan mobil kecil sebagai x, mobil besar sebagai y.
Luas parkir $1760$ m$^{2}$ $:4x+20y\le1760$ $\rightarrow x+5y\le440$……(Garis I)
Daya tampung lahan parkir 200 kendaraan: $x+y\le200$ ………(Garis II)
Fungsi objektifnya adalah hasil parkiran: $f(x,y)=1000x+2000y$
Perhatikan gambar dibawah ini!

Titik potong antara garis $x+y=200$ dan garis $x+5y=440$ adalah $(140,60)$
Titik ujung penyelesaian yaitu $(0,0),\,(200,0),\,(140,60),\,(0,88)$
Masukkan koordinat titik-titik uji / warna merah ke $f(x,y)=1000x+2000y.$
$f(0,0)=1000(0)+200(0)=0$
$f(200,0)=1000(200)+2000(0)$$=200.000$
$f(0,88)=1000(0)+2000(88)$$=176.000$
$f(140,60)=1000(140)+2000(60)=260.000$ (maksimum)
Jadi hasil parkiran maksimum adalah Rp. $260.000,00.$
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Seorang pedagang menjual buah mangga dan pisang dengan menggunakan gerobak. Pedagang tersebut membeli mangga dengan harga Rp 8.000,00/kg dan pisang Rp 6.000,00/kg. Modal yang tersedia Rp 1.200.000,00 dan gerobaknya hanya dapat menampung mangga dan pisang sebanyak 180 kg. Jika harga jual mangga Rp 9.200,00/kg dan pisang Rp 7.000,00/kg, maka laba maksimum yang diperoleh pedagang tersebut adalah…
BetulKarena ditanya laba maksimum, maka fungsi tujuannya adalah keuntungan dari menjual buah mangga dan buah pisang perkilonya.
Berikut untung penjualan :
Mangga $=9.200-8.000=1.200.$ Pisang $=7.000-6000=1.000$
Misalkan : mangga = x dan pisang = y
Fungsi tujuannya adalah : $F(x,y)=1.200x+1.000y$
Model matematika atau sistem pertidaksamaan yang memenuhi soal tersebut adalah :
$x+y\leq180$
$8.000x+6.000y\leq1.200.000$$\rightarrow4x+3y\leq600$
$x\leq0;\, y\leq0$
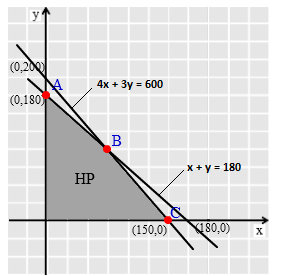
Perhatikan gambar berikut ini!

Perpotongan antara garis $4x+3y=600$ dan $x+y=180$ adalah titik $B(60,120)$
$F(x,y)=1.200x+1.000y$
$F(A)=F(0,180)$$=1.200(0)+1.000(180)=180.000$
$F(B)=F(60,120)$$=1.200(60)+1.000(120)=192.000$
$F(C)=F(150,0)$$=1.200(150)=180.000$
Jadi laba maksimum yang diperoleh pedagang buah adalah Rp $192.000,00.$
SalahKarena ditanya laba maksimum, maka fungsi tujuannya adalah keuntungan dari menjual buah mangga dan buah pisang perkilonya.
Berikut untung penjualan :
Mangga $=9.200-8.000=1.200.$ Pisang $=7.000-6000=1.000$
Misalkan : mangga = x dan pisang = y
Fungsi tujuannya adalah : $F(x,y)=1.200x+1.000y$
Model matematika atau sistem pertidaksamaan yang memenuhi soal tersebut adalah :
$x+y\leq180$
$8.000x+6.000y\leq1.200.000$$\rightarrow4x+3y\leq600$
$x\leq0;\, y\leq0$
Perhatikan gambar berikut ini!

Perpotongan antara garis $4x+3y=600$ dan $x+y=180$ adalah titik $B(60,120)$
$F(x,y)=1.200x+1.000y$
$F(A)=F(0,180)$$=1.200(0)+1.000(180)=180.000$
$F(B)=F(60,120)$$=1.200(60)+1.000(120)=192.000$
$F(C)=F(150,0)$$=1.200(150)=180.000$
Jadi laba maksimum yang diperoleh pedagang buah adalah Rp $192.000,00.$
Latihan Soal Aplikasi Program Linear (Sukar)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Seorang pedagang skuter ingin membeli 25 sepeda untuk persediaan. Ia ingin membeli skuter merk A dengan harga Rp1.500.000,00 per buah dan skuter merk B dengan harga Rp2.000.000,00 per buah. Ia merencanakan tidak akan mengeluarkan uang lebih dari Rp42.000.000,00. Jika keuntungan sebuah skuter merk A Rp500.000,00 dan sebuah skuter merk B Rp600.000,00, maka keuntungan maksimum yang diterima pedagang adalah…
BetulMisalkan skuter merk A = x dam skuter merk B = y

Model pertidaksamaan yang memenuhi :
$x+y\leq25$
$1.500.000x+2.000.000y\leq42.000.000$$\rightarrow3x+4y\leq84$
$F(x,y)=500.000x+600.000y$
Perhatikan gambar berikut!

$F(x,y)=500.000x+600.000y$
$F(25,0)=12.500.000,00$
$F(0,21)=12.600.000,00$
$F(16,9)=13.400.000,00$ (maksimum)
Jadi keuntungan maksimumnya adalah Rp $13.400.000,00.$
SalahMisalkan skuter merk A = x dam skuter merk B = y

Model pertidaksamaan yang memenuhi :
$x+y\leq25$
$1.500.000x+2.000.000y\leq42.000.000$$\rightarrow3x+4y\leq84$
$F(x,y)=500.000x+600.000y$
Perhatikan gambar berikut!

$F(x,y)=500.000x+600.000y$
$F(25,0)=12.500.000,00$
$F(0,21)=12.600.000,00$
$F(16,9)=13.400.000,00$ (maksimum)
Jadi keuntungan maksimumnya adalah Rp $13.400.000,00.$
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Seorang pemiliki toko ingin mengisi tokonya dengan sepatu laki-laki paling sedikit 100 pasang dan sepatu wanita paling sedikit 150 pasang. Toko tersebut dapat memuat 400 pasang sepatu. Keuntungan setiap pasang sepatu laki-laki Rp. 1000 dan setiap pasang sepatu wanita Rp. 500. Jika banyaknya sepatu laki-laki tidak boleh melebihi 150 pasang, keuntungan terbesar yang dapat diperoleh adalah…
BetulMisal x = sepatu laki-laki dan y = sepatu perempuan
Pertidaksamaan yang memenuhi adalah :
$100\le x\le150$
$x+y\le400$
$y\ge15$
$F(x,y)=1000x+500y$
Perhatikan gambar berikut!

Daerah yang diarsir adalah daerah penyelesaian. Titik A, B, C, dan D adalah titik penyelesaian.
$A(100,150),\, B(150,150),\, C(150,250),\, D(100,300)$
$F(x,y)=1000x+500y$
$F(100,150)=1000(100)+500(150)=175.000$ (minimum)
$F(150,150)=1000(150)+500(150)=225.000$
$F(150,250)=1000(150)+500(250)=275.000$ (maksimum)
$F(100,300)=1000(100)+500(300)=250.000$
Jadi nilai maksimumnya adalah Rp. $275.000,00.$
SalahMisal x = sepatu laki-laki dan y = sepatu perempuan
Pertidaksamaan yang memenuhi adalah :
$100\le x\le150$
$x+y\le400$
$y\ge15$
$F(x,y)=1000x+500y$
Perhatikan gambar berikut!

Daerah yang diarsir adalah daerah penyelesaian. Titik A, B, C, dan D adalah titik penyelesaian.
$A(100,150),\, B(150,150),\, C(150,250),\, D(100,300)$
$F(x,y)=1000x+500y$
$F(100,150)=1000(100)+500(150)=175.000$ (minimum)
$F(150,150)=1000(150)+500(150)=225.000$
$F(150,250)=1000(150)+500(250)=275.000$ (maksimum)
$F(100,300)=1000(100)+500(300)=250.000$
Jadi nilai maksimumnya adalah Rp. $275.000,00.$
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Menjelang hari raya Idul Adha, Pak Andi hendak menjual sapi dan kerbau. Harga seekor sapi dan kerbau berturut-turut Rp 9.000.000,00 dan Rp 8.000.000,00. Modal yang dimiliki pak Andi adalah Rp 124.000.000,00. Pak Andi menjual sapi dan kerbau dengan harga berturut-turut Rp 10.300.000,00 dan Rp 9.200.000,00. Kandang yang ia miliki hanya dapat menampung tidak lebih dari 15 ekor. Agar mencapai keuntungan maksimum, banyak sapi dan kerbau yang harus dibeli pak Andi adalah…
BetulKarena ditanya keuntungan, tentu fungsi tujuannya adalah besar keuntungan dari penjualan sapi dan kerbau.
Untung sapi = Rp 10.300.000,00 – Rp 9.000.000,00 = Rp 1.300.000,00
Untung kerbau = Rp 9.200.000,00 – Rp 8.000.000,00 = Rp 1.200.000,00
Misalkan banyak sapi = x dan banyak kerbau = y, maka fungsi objektifnya : $f(x,y)=1.300.000x+1.200.000y$
Model matematika yang memenuhi soal adalah :
$x+y\leq15$
$9.000.000x+8.000.000y\leq124.000.000$$\Rightarrow9x+8y\leq124$
$x\geq0;\, y\geq0$
Perhatikan gambar dibawah ini!

Titik A, B, dan C titik ujung penyelesaian.
Titik B adalah titik perpotongan antara garis $x+y=15$ dan garis $9x+8y=124$ yaitu $B(4,11)$
$F(x,y)=1.300.000x+1.200.000y$
$F(A)=F(0,15)$$=1.300.000(0)+1.200.000(15)$$=18.000.000$
$F(B)=F(4,11)$$=1.300.000(4)+1.200.000(11)$$=18.400.000$ (maksimum)
$F(C)=F(13,0)$$=13.000.000(13)+1.200.000(0)$$=16.900.000$ (minimum)
Jadi, agar keuntungannya maksimum, jumlah sapi dan kerbau yang harus dibeli pak Andi adalah 4 ekor sapi dan 11 ekor kerbau.
SalahKarena ditanya keuntungan, tentu fungsi tujuannya adalah besar keuntungan dari penjualan sapi dan kerbau.
Untung sapi = Rp 10.300.000,00 – Rp 9.000.000,00 = Rp 1.300.000,00
Untung kerbau = Rp 9.200.000,00 – Rp 8.000.000,00 = Rp 1.200.000,00
Misalkan banyak sapi = x dan banyak kerbau = y, maka fungsi objektifnya : $f(x,y)=1.300.000x+1.200.000y$
Model matematika yang memenuhi soal adalah :
$x+y\leq15$
$9.000.000x+8.000.000y\leq124.000.000$$\Rightarrow9x+8y\leq124$
$x\geq0;\, y\geq0$
Perhatikan gambar dibawah ini!

Titik A, B, dan C titik ujung penyelesaian.
Titik B adalah titik perpotongan antara garis $x+y=15$ dan garis $9x+8y=124$ yaitu $B(4,11)$
$F(x,y)=1.300.000x+1.200.000y$
$F(A)=F(0,15)$$=1.300.000(0)+1.200.000(15)$$=18.000.000$
$F(B)=F(4,11)$$=1.300.000(4)+1.200.000(11)$$=18.400.000$ (maksimum)
$F(C)=F(13,0)$$=13.000.000(13)+1.200.000(0)$$=16.900.000$ (minimum)
Jadi, agar keuntungannya maksimum, jumlah sapi dan kerbau yang harus dibeli pak Andi adalah 4 ekor sapi dan 11 ekor kerbau.
-
Pertanyaan ke 4 dari 5
4. Pertanyaan
Sebuah perusahaan properti memproduksi dua macam lemari pakaian yaitu tipe lux dan tipe sport dengan menggunakan 2 bahan dasar yang sama yaitu kayu jati dan cat pernis. Untuk memproduksi 1 unit tipe lux dibutuhkan 10 batang kayu jati dan 3 kaleng cat pernis, sedangkan untuk memproduksi 1 unit tipe sport dibutuhkan 6 batang kayu jati dan 1 kaleng cat pernis. Biaya produksi tipe lux dan tipe sport masing-masing adalah Rp 40.000 dan Rp 28.000 per unit. Untuk satu periode produksi, perusahaan menggunakan paling sedikit 120 batang kayu jati dan 24 kaleng cat pernis. Bila perusahaan harus memproduksi lemari tipe lux paling sedikit 2 buah dan tipe sport paling sedikit 4 buah, banyak lemari tipe lux dan tipe sport yang harus diproduksi agar biaya produksinya minimum adalah…
BetulKarena yang ditanya adalah biaya produksi minimum, maka ongkos produksi masing-masing tipe lemari merupakan fungsi tujuannya.
Misalkan tipe lux = x dan tipe sport = y, maka fungsi tujuannya adalah sebagai berikut :
$F(x,y)=40.000x+28.000y$

Model pertidaksamaan yang memenuhi adalah :
$x\geq2$
$y\geq4$
$10x+6y\geq120\rightarrow5x+3y\geq60$
$3x+y\geq24$
Perhatikan gambar dibawah ini!

Titik A, B, dan C adalah titik ujung penyelesaian.
Titik A adalah titik perpotongan antara garis $x=2$ dangaris $3x+y=24$ yaitu $A(2,18)$
Titik B adalah titik perpotongan antara garis $3x+y=24$ dan garis $5x+3y=60$ yaitu $B(3,15)$
Titik C adalah titik perpotongan antara garis $y=4$ dan garis $5x+3y=60$ yaitu $C(9,4)$
$F(x,y)=40.000x+28.000y$
$F(2,18)=40.000(2)+28.000(18)=584.000$
$F(3,15)=40.000(3)+28.000(15)=540.000$
$F(9,4)=40.000(9)+28.000(4)=482.000$
Jadi agar biaya produksi minimum, perusahaan sebaiknya memproduksi 9 buah lemari tipe lux dan 4 buah lemari tipe sport dengan biaya produksi Rp $482.000,00.$
SalahKarena yang ditanya adalah biaya produksi minimum, maka ongkos produksi masing-masing tipe lemari merupakan fungsi tujuannya.
Misalkan tipe lux = x dan tipe sport = y, maka fungsi tujuannya adalah sebagai berikut :
$F(x,y)=40.000x+28.000y$

Model pertidaksamaan yang memenuhi adalah :
$x\geq2$
$y\geq4$
$10x+6y\geq120\rightarrow5x+3y\geq60$
$3x+y\geq24$
Perhatikan gambar dibawah ini!

Titik A, B, dan C adalah titik ujung penyelesaian.
Titik A adalah titik perpotongan antara garis $x=2$ dangaris $3x+y=24$ yaitu $A(2,18)$
Titik B adalah titik perpotongan antara garis $3x+y=24$ dan garis $5x+3y=60$ yaitu $B(3,15)$
Titik C adalah titik perpotongan antara garis $y=4$ dan garis $5x+3y=60$ yaitu $C(9,4)$
$F(x,y)=40.000x+28.000y$
$F(2,18)=40.000(2)+28.000(18)=584.000$
$F(3,15)=40.000(3)+28.000(15)=540.000$
$F(9,4)=40.000(9)+28.000(4)=482.000$
Jadi agar biaya produksi minimum, perusahaan sebaiknya memproduksi 9 buah lemari tipe lux dan 4 buah lemari tipe sport dengan biaya produksi Rp $482.000,00.$
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Jika luas bidang yang dibatasi oleh garis $y=\frac{3}{2}x$, $y=500-x$, dan sumbu x antara $x=0$
dan $x=500$ menyatakan banyaknya yang berpenghasilan antara a ribu dan b ribu rupiah, karyawan yang berpenghasilan diatas Rp. 400.000 rupiah adalah…BetulPerhatikan gambar dibawah ini!

Perpotongan antara garis $y=\frac{3}{2}x$ dan $y=500-x$ terjadi di titik $A(200,300)$
* Luas segitiga OAE menunjukan banyaknya karyawan suatu pabrik, yaitu : $\frac{1}{2}\cdot500\cdot300=75.000.$
* Luas segitiga CDE menunjukan banyaknya karyawan yang berpenghasilan diatas Rp. 400.000, yaitu :
$\frac{1}{2}\cdot100\cdot100=5.000.$Jadi anyaknya karyawan yang berpenghasilan diatas Rp. $400.000$ yaitu $\frac{5.000}{75.000}=\frac{1}{15}$ bagian.
SalahPerhatikan gambar dibawah ini!

Perpotongan antara garis $y=\frac{3}{2}x$ dan $y=500-x$ terjadi di titik $A(200,300)$
* Luas segitiga OAE menunjukan banyaknya karyawan suatu pabrik, yaitu : $\frac{1}{2}\cdot500\cdot300=75.000.$
* Luas segitiga CDE menunjukan banyaknya karyawan yang berpenghasilan diatas Rp. 400.000, yaitu :
$\frac{1}{2}\cdot100\cdot100=5.000.$Jadi anyaknya karyawan yang berpenghasilan diatas Rp. $400.000$ yaitu $\frac{5.000}{75.000}=\frac{1}{15}$ bagian.