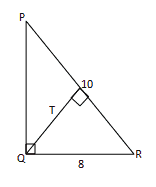Masih sering bingung dengan rmateri teorema pythagoras? Yuk, simak penjelasan lengkapnya lewat video yang ada di sini. Setelahnya, kamu juga bisa mengerjakan latihan soal yang telah disediakan untuk mengasah kemampuan belajarmu.
Di sini, kamu akan belajar tentang Teorema Pythagoras melalui video yang dibawakan oleh Bapak Anton Wardaya. Kamu akan diajak untuk memahami materi hingga metode menyelesaikan soal.
Selain itu, kamu juga akan mendapatkan latihan soal interaktif dalam 3 tingkat kesulitan (mudah, sedang, sukar). Dengan begitu, kamu bisa langsung mempraktikkan materi yang telah dijelaskan.
Sekarang, kamu bisa mulai belajar dengan 2 video dan 3 set latihan soal yang ada di halaman ini. Apabila materi ini berguna, bagikan ke teman atau rekan kamu supaya mereka juga mendapatkan manfaatnya.
Kamu dapat download modul & contoh soal serta kumpulan latihan soal lengkap dalam bentuk pdf pada list dibawah ini:
Pembuktian Rumus Pythagoras
Contoh Soal Pythagoras
Latihan Soal Pythagoras (Mudah)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
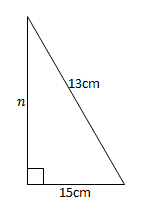
Nilai dari $n$ pada gambar dibawah ini adalah…
 Betul
Betul$\begin{aligned}n & =\sqrt{13^{2}-5^{2}}\\
& =\sqrt{169-25}\\
& =\sqrt{144}\\
& =12
\end{aligned}
$Salah$\begin{aligned}n & =\sqrt{13^{2}-5^{2}}\\
& =\sqrt{169-25}\\
& =\sqrt{144}\\
& =12
\end{aligned}
$ -
Pertanyaan ke 2 dari 5
2. Pertanyaan
Berikut ini adalah ukuran beerapa sisi segitiga:
i. $3,4,6$
ii. $\sqrt{3},\sqrt{3},\sqrt{6}$
iii. $15,20,26$
iv. $\sqrt{7},\sqrt{8},\sqrt{15}$Dari ukuran diatas yang dapat membentuk segitiga siku-siku adalah…
Betuli. $3^{2}+4^{2}…6^{2}$
$9+16…36$
$25\neq36$
ii. $\sqrt{3}^{2}+\sqrt{3}^{2}…\sqrt{6}^{2}$
$3+3=6$
iii. $15^{2}+20^{2}…26^{2}$
$225+400\neq676$
iv. $\sqrt{7}^{2}+(\sqrt{8})^{2}…(\sqrt{15})^{2}$
$7+8=15$
Salahi. $3^{2}+4^{2}…6^{2}$
$9+16…36$
$25\neq36$
ii. $\sqrt{3}^{2}+\sqrt{3}^{2}…\sqrt{6}^{2}$
$3+3=6$
iii. $15^{2}+20^{2}…26^{2}$
$225+400\neq676$
iv. $\sqrt{7}^{2}+(\sqrt{8})^{2}…(\sqrt{15})^{2}$
$7+8=15$
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Dari tigaan-tigaan bilangan berikut yang merupakan tripel pythagoras adalah…
BetulPembuktian c:
$15^{2}+20^{2}…25^{2}$
$225+400=625$
SalahPembuktian c:
$15^{2}+20^{2}…25^{2}$
$225+400=625$
-
Pertanyaan ke 4 dari 5
4. Pertanyaan
Diketahui ukuran $\vartriangle ABC$ adalah $AB=5$ cm, $BC=12$ cm. $\vartriangle ABC$ akan membentuk segitiga siku-siku jika panjang $AC=$…cm.
Betul$\begin{aligned}AC & =\sqrt{AB^{2}+BC^{2}}\\
& =\sqrt{5^{2}+12^{2}}\\
& =\sqrt{25+144}\\
& =\sqrt{169}\\
& =13
\end{aligned}
$Salah$\begin{aligned}AC & =\sqrt{AB^{2}+BC^{2}}\\
& =\sqrt{5^{2}+12^{2}}\\
& =\sqrt{25+144}\\
& =\sqrt{169}\\
& =13
\end{aligned}
$ -
Pertanyaan ke 5 dari 5
5. Pertanyaan
Perhatikan Gambar dibawah ini!

Nilai $n$ adalah…cm.
Betul$\begin{aligned}n^{2}+n^{2} & =12^{2}\\
2n^{2} & =144\\
n^{2} & =72\\
n & =\sqrt{72}\\
& =6\sqrt{2}
\end{aligned}
$Salah$\begin{aligned}n^{2}+n^{2} & =12^{2}\\
2n^{2} & =144\\
n^{2} & =72\\
n & =\sqrt{72}\\
& =6\sqrt{2}
\end{aligned}
$
Latihan Soal Pythagoras (Sedang)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Panjang sisi belah ketupat masing-masing adalah $20$ cm. Jika panjang salah satu diagonalnya $32$ cm, maka panjang diagonal yang kedua adalah…cm.
Betul
$\begin{aligned}n & =\sqrt{20^{2}-16^{2}}\\
& =\sqrt{400-256}\\
& =\sqrt{144}\\
& =12
\end{aligned}
$Diagonal ke dua $=12+12=24.$
Salah
$\begin{aligned}n & =\sqrt{20^{2}-16^{2}}\\
& =\sqrt{400-256}\\
& =\sqrt{144}\\
& =12
\end{aligned}
$Diagonal ke dua $=12+12=24.$
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Keliling belah ketupat yang panjang diagobalnya $6$ cm dan $8$ cm adalah…cm.
Betul
$\begin{aligned}n & =\sqrt{3^{2}+4^{2}}\\
& =\sqrt{9+16}\\
& =\sqrt{25}\\
& =5
\end{aligned}
$$\begin{aligned}K & =4n\\
& =4\times5\\
& =20\mbox{ cm}
\end{aligned}
$Salah
$\begin{aligned}n & =\sqrt{3^{2}+4^{2}}\\
& =\sqrt{9+16}\\
& =\sqrt{25}\\
& =5
\end{aligned}
$$\begin{aligned}K & =4n\\
& =4\times5\\
& =20\mbox{ cm}
\end{aligned}
$ -
Pertanyaan ke 3 dari 5
3. Pertanyaan
Keliling belah ketupat $80$ cm. Jika panjang salah satu diagonalnya $32$ cm, maka luas belah ketupat tersebut adalah…cm$^{2}.$
Betul$\begin{aligned}4a & =80\\
a & =20
\end{aligned}
$$\begin{aligned}n & =\sqrt{a^{2}-16^{2}}\\
& =\sqrt{20^{2}-16^{2}}\\
& =\sqrt{410-256}\\
& =\sqrt{144}\\
& =12
\end{aligned}
$Diagonal $=12\times2=24$ cm
$\begin{aligned}L & =\frac{1}{2}\times24\times32\\
& =12\times32\\
& =384\mbox{ cm}{}^{2}
\end{aligned}
$Salah$\begin{aligned}4a & =80\\
a & =20
\end{aligned}
$$\begin{aligned}n & =\sqrt{a^{2}-16^{2}}\\
& =\sqrt{20^{2}-16^{2}}\\
& =\sqrt{410-256}\\
& =\sqrt{144}\\
& =12
\end{aligned}
$Diagonal $=12\times2=24$ cm
$\begin{aligned}L & =\frac{1}{2}\times24\times32\\
& =12\times32\\
& =384\mbox{ cm}{}^{2}
\end{aligned}
$ -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Panjang diagonal sebuah persegi adalah $18$ cm. Luas persegi tersebut adalah…cm$^{2}.$
Betul
$\begin{aligned}n^{2}+n^{2} & =18^{2}\\
2n^{2} & =18\times18
\end{aligned}
$$\begin{aligned}n & =\sqrt{18\times9}\\
& =\sqrt{9\times2\times9}\\
& =9\sqrt{2}
\end{aligned}
$$\begin{aligned}L & =9\sqrt{2}\times9\sqrt{2}\\
& =81\times2\\
& =162
\end{aligned}
$Salah
$\begin{aligned}n^{2}+n^{2} & =18^{2}\\
2n^{2} & =18\times18
\end{aligned}
$$\begin{aligned}n & =\sqrt{18\times9}\\
& =\sqrt{9\times2\times9}\\
& =9\sqrt{2}
\end{aligned}
$$\begin{aligned}L & =9\sqrt{2}\times9\sqrt{2}\\
& =81\times2\\
& =162
\end{aligned}
$ -
Pertanyaan ke 5 dari 5
5. Pertanyaan
Panjang sebuah persegi panjang adalah $\frac{3}{2}$ dari lebarnya. Jika panjang persegi panjang adalah $12$ cm, maka panjang diagonalnya adalah…cm.
Betul$p=\frac{3}{2}l\Leftrightarrow l=\frac{2}{3}p$
$l=\frac{2}{3}\times12$
$l=8$
Panjang diagonal $=\sqrt{12^{2}+8^{2}}$
$=\sqrt{144+64}$
$=\sqrt{208}$
$=4\sqrt{13}.$
Salah$p=\frac{3}{2}l\Leftrightarrow l=\frac{2}{3}p$
$l=\frac{2}{3}\times12$
$l=8$
Panjang diagonal $=\sqrt{12^{2}+8^{2}}$
$=\sqrt{144+64}$
$=\sqrt{208}$
$=4\sqrt{13}.$
Latihan Soal Pythagoras (Sukar)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Panjang kedua diagonal belah ketupat memiliki perbandingan $3:4.$ Jika jumlah kedua diagonal $28$ cm, maka ukuran sisi belah ketupat tersebut adalah…cm.
Betul$d_{1}:d_{2}=3:4$
$d_{1}+d_{2}=28$
$\begin{aligned}d_{1} & =\frac{3}{7}\times28\\
& =12
\end{aligned}
$$\begin{aligned}d_{2} & =\frac{4}{7}\times28\\
& =16
\end{aligned}
$$\begin{aligned}\mbox{Ukuran sisi } & =\sqrt{6^{2}+8^{2}}\\
& =\sqrt{100}\\
& =10\mbox{ cm.}
\end{aligned}
$Salah$d_{1}:d_{2}=3:4$
$d_{1}+d_{2}=28$
$\begin{aligned}d_{1} & =\frac{3}{7}\times28\\
& =12
\end{aligned}
$$\begin{aligned}d_{2} & =\frac{4}{7}\times28\\
& =16
\end{aligned}
$$\begin{aligned}\mbox{Ukuran sisi } & =\sqrt{6^{2}+8^{2}}\\
& =\sqrt{100}\\
& =10\mbox{ cm.}
\end{aligned}
$ -
Pertanyaan ke 2 dari 5
2. Pertanyaan
Sebuah kapal bergerak dari A menuju ke arah timur (B) sejauh $50$ km. Kemudian dari B menuju ke arah utar (C) sejauh $120$ km. Jarak terpendek dari $A$ menuju $C$ adalah…km.
Betul
$\begin{aligned}n & =\sqrt{50^{2}+120^{2}}\\
& =\sqrt{2500+14400}\\
& =\sqrt{16900}\\
& =130
\end{aligned}
$Salah
$\begin{aligned}n & =\sqrt{50^{2}+120^{2}}\\
& =\sqrt{2500+14400}\\
& =\sqrt{16900}\\
& =130
\end{aligned}
$ -
Pertanyaan ke 3 dari 5
3. Pertanyaan
Diketahui $\triangle PQR$ siku-siku di titik $Q$. Jika panjang $PR=10$ cm dan $QR=8$ cm, maka panjang garis tinggi yang ditarik dari $Q$ menuju $PR$ adalah…cm.
Betul
$\begin{aligned}PQ & =\sqrt{10^{2}-8^{2}}\\
& =\sqrt{100-64}\\
& =\sqrt{36}\\
& =6
\end{aligned}
$$\frac{1}{2}\times PQ\times QR=\frac{1}{2}\times QT\times PR$
$\frac{1}{2}\times6\times8=\frac{1}{2}\times QT\times10$
$QT=\frac{48}{10}$$=4,8$
Salah
$\begin{aligned}PQ & =\sqrt{10^{2}-8^{2}}\\
& =\sqrt{100-64}\\
& =\sqrt{36}\\
& =6
\end{aligned}
$$\frac{1}{2}\times PQ\times QR=\frac{1}{2}\times QT\times PR$
$\frac{1}{2}\times6\times8=\frac{1}{2}\times QT\times10$
$QT=\frac{48}{10}$$=4,8$
-
Pertanyaan ke 4 dari 5
4. Pertanyaan
Pada gambar dibawah ini, $QR=30$ cm.

Jika $PR=50$ cm, maka $QS=$…cm.
Betul$\begin{aligned}PQ & =\sqrt{PR^{2}-QR^{2}}\\
& =\sqrt{50^{2}-30^{2}}\\
& =\sqrt{2500-900}\\
& =\sqrt{1600}\\
& =40
\end{aligned}
$$\frac{1}{2}\times PR\times QS=\frac{1}{2}\times PQ\times QR$
$\frac{1}{2}\times50\times QS=\frac{1}{2}\times40\times30$
$5\times QS=4\times30$
$QS=24$
Salah$\begin{aligned}PQ & =\sqrt{PR^{2}-QR^{2}}\\
& =\sqrt{50^{2}-30^{2}}\\
& =\sqrt{2500-900}\\
& =\sqrt{1600}\\
& =40
\end{aligned}
$$\frac{1}{2}\times PR\times QS=\frac{1}{2}\times PQ\times QR$
$\frac{1}{2}\times50\times QS=\frac{1}{2}\times40\times30$
$5\times QS=4\times30$
$QS=24$
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
$\triangle ABC$ adalah segitiiga siku-siku samakaki. Jika $AB=AC$ dan panjang $BC=16$ cm, maka luas $\triangle$…cm$^{2}.$
Betul
$n^{2}+n^{2}=16^{2}$
$2n^{2}=16\times16$
$n^{2}=8\times16$
$\begin{aligned}n & =\sqrt{8\times16}\\
& =\sqrt{64\times2}\\
& =8\sqrt{2}
\end{aligned}
$$\begin{aligned}L & =\frac{1}{2}\times8\sqrt{2}\times8\sqrt{2}\\
& =4\sqrt{2}\times8\sqrt{2}\\
& =32\times2\\
& =64
\end{aligned}
$Salah
$n^{2}+n^{2}=16^{2}$
$2n^{2}=16\times16$
$n^{2}=8\times16$
$\begin{aligned}n & =\sqrt{8\times16}\\
& =\sqrt{64\times2}\\
& =8\sqrt{2}
\end{aligned}
$$\begin{aligned}L & =\frac{1}{2}\times8\sqrt{2}\times8\sqrt{2}\\
& =4\sqrt{2}\times8\sqrt{2}\\
& =32\times2\\
& =64
\end{aligned}
$