Ketidakpastian merupakan salah satu materi fisika yang cukup menarik untuk dibahas. Kalau kebetulan kamu ingin belajar tentang materi ini lebih dalam, simak penjelasan lengkapnya berikut. Kami juga telah menyediakan soal latihan yang bisa dikerjakan untuk mengasah kemampuanmu.
Lewat pembahasan ini, kamu bisa belajar mengenai Ketidakpastian. Kamu akan diajak untuk memahami materi dan tentang metode menyelesaikan soal.
Kamu juga akan memperoleh latihan soal interaktif yang tersedia dalam tiga tingkat kesulitan, yaitu mudah, sedang, dan sukar. Tertarik untuk mempelajarinya?
Sekarang, kamu bisa mulai mempelajari materi lewat uraian berikut. Apabila materi ini berguna, bagikan ke teman-teman kamu supaya mereka juga mendapatkan manfaatnya.
Kamu dapat download modul & kumpulan soal dalam bentuk pdf pada link dibawah ini:
Definisi
Ketidakpastian dalam pengukuran disebabkan oleh adanya kesalahan dalam pengukuran.
Ketidakpastian Pengukuran
A. Kesalahan Pengukuran
Suatu pengukuran selalu disertai oleh ketidakpastian pengukuran yang disebabkan oleh adanya kesalahan dalam pengukuran. Kesalahan adalah penyimpangan nilai yang diukur dari nilai sebenarnya. Kesalahan dapat dikelompokkan menjadi tiga kelompok.
1. Kesalahan umum
Kesalahan umum adalah kesalahan yang diakibatkan oleh keterbatasan pada pengamat. Misalnya kurang terampilnya pengamat menggunakan alat ukur, kesalahan membaca hasil pengukuran dan kesalahan-kesalahan paralaks.
2. Kesalahan Sistematik
Kesalahan sistematik diakibatkan oleh kesalahan pada instrumen yang digunakan. Beberapa instrumen mungkin dipengaruhi oleh kondisi lingkungan seperti suhu dan tekanan ruangan, medan listrik, medan magnet dan medan gravitasi.
3. Kesalahan acak
Kesalahan acak merupakan kesalahan yang berasal dari pengaruh faktor-faktor yang tidak dapat diprediksi dan hanya bersifat sementara. Kesalahan acak terjadi secara kebetulan atau tanpa disengaja dan bervariasi dari pengujian ke pengujian lainnya. Kesalahan acak sulit dihindari disebabkan oleh fluktuasi yang tidak dapat diduga. Sebab-sebab kesalahan acak tidak dapat diketahui dengan pasti tetapi merupakan bagian dari pengaruh yang memiliki kontribusi kesalahan dalam pelaksanaan pengujian.
Hasil pengukuran suatu besaran dituliskan sebagai $x=x_{0}\pm\Delta x$ dengan $x$ adalah nilai pendekatan terhadap nilai benar $x_{0}$ dan $\Delta x$ adalah ketidakpastiannya.
B. Ketidakpastian
Ada dua jenis ketidakpastian pengukuran, yaitu pengukuran tunggal dan pengukuran berulang.
1. Ketidakpastian pengukuran tungal
Pengukuran tunggal merupakan pengukuran yang hanya dilakukan satu kali. Pada pengukuran tunggal, nilai yang dijadikan pengganti nilai benar adalah hasil pengukuran itu sendiri dan ketidakpastiannya diperoleh dari setengah nilai skala terkecil (nst) instrumen yang digunakan.
Misalkan seorang pengamat mengukur panjang pensil menggunakan mistar diperoleh nilai benar sebesar 12 cm. Skala terkecil dari mistar adalah 1 mm atau 0,1 cm maka $\Delta x=\frac{1}{2}\times\mbox{nst}=\frac{1}{2}\times0,1$. Hasil pengukuran tunggal ini dituliskan sebagai $L=12\pm0,05$ cm.
2. Ketidakpastain pengukuran berulang
Agar mendapatkan hasil pengukuran yang akurat, harus dilakukan pengukuran secara berulang. Pada pengukuran berulang nilai terbaik untuk menggantikan nilai benar $x_{0}$ adalah nilai rata – rata dari data yang diperoleh ($\bar{x}$). Sedangkan untuk nilai ketidakpastiannya ($\Delta x$) dapat digantikan oleh nilai simpangan baku nilai rata-rata sampel. Secara matematis dapat ditulis sebagai berikut.
$\bar{x}=\frac{x_{1}+x_{2}+x_{3}+…..+x_{n}}{N}=\frac{\sum x_{i}}{N}$
$\Delta x=\frac{1}{N}\sqrt{\frac{N\sum x_{i}^{2}-(\sum x_{i})^{2}}{N-1}}$
Keterangan:
$\bar{x}$ : hasil pengukuran yang mendekati nilai benar
$\Delta x$ : ketidakpastian pengukuran
$N$ : banyaknya pengukuran yang dilakukan.
Ketidakpastian menunjukkan seberapa dekat hasil pengukuran mendekati nilai sebenarnya. Semakin kecil nilainya maka semakin dekat hasil pengukuran dengan nilai sebenarnya. Pada pengukuran tunggal ketidak pastian $\Delta x$ disebut ketidakpastian mutlak.
Pada pengukuran berulang dikenal istilah ketidak pastian relatif, yaitu perbandingan ketidakpastian pengukuran berulang dengan nilai rata-rata pengukuran.
ketidakpastian relatif $=\frac{\Delta x}{\bar{x}}\times100%$
Nilai ketidakpastian relatif menentukan banyaknya angka yang boleh disertakan pada laporan hasil pengukuran. Aturan banyaknya angka yang dapat dilaporkan dalam pengukuran berulang adalah sebagai berikut.
- relatif 10 % berhak atas dua angka
- relatif 1%berhak atas tiga angka
- relatif 0,1% berhak atas empat angka
Perhitungan Ketidakpastian
Dalam fisika sering dijumpai perhitungan yang melibatkan beberapa besaran hasil pengukuran yang mengandung nilai ketidak pastian. Hal ini berarti bahwa perhitungan juga melibatkan ketidak pastian. Ada empat aturan dasar dalam perhitungan yang melibatkan teori ketidakpastian fisika.
1. Aturan Penjumlahan dan Pengurangan
Jika dua besaran dijumlahkan atau dikurangkan aturannya adalah tambahkan ketidakpastian mutlaknya. Secara matematis dituliskan:
$\left(x\pm\Delta x\right)+\left(y\pm\Delta y\right)=(x+y)\pm(\Delta x+\Delta y)$
$\left(x\pm\Delta x\right)-\left(y\pm\Delta y\right)=(x-y)\pm(\Delta x+\Delta y)$
Contoh:
Penjumlahan: $(6,0\pm0,5)\mbox{ m}+(3,5\pm0,1)\mbox{ m}=\left(9,5\pm0,6\right)\mbox{m}$
Pengurangan: $(6,0\pm0,5)\mbox{ m}-(3,5\pm0,1)\mbox{ m}=\left(2,5\pm0,6\right)\mbox{m}$
2. Aturan Perkalian dan Pembagian
Jika dua besaran terlibat operasi perkalian dan pembagian maka tambahkan ketidak pastian relatifnya. Misal untuk menghitung luas persegi panjang $L=p\times l$ dengan $p=x\pm\Delta x$ dan $l=y\pm\Delta y$. Ketidakpastian luas persegi panjang dituliskan sebagai:
$\frac{\Delta L}{L}=\frac{\Delta x}{x}+\frac{\Delta y}{y}$
Contoh:
Ukuran sebuah persegi panjang adalah $2\pm0,1$ cm dan $10\pm0,5$ cm, maka ketidak pastian luasnya adalah
$\begin{alignedat}{1}\Delta L & =\left(\frac{\Delta x}{x}+\frac{\Delta y}{y}\right)L\\
\Delta L & =\left(\frac{0,1}{2}+\frac{0,5}{10}\right)\times20\\
\Delta L & =0,1\times20\\
\Delta L & =2
\end{alignedat}
$
Jadi luas persegi panjang dapat dituliskan sebagai $L=\left(20\pm2\right)\mbox{cm}^{2}$
3. Aturan Pangkat
Aturan pangkat sebenarnya sama dengan aturan perkalian, namun karena yang dikalikan adalah bilangan yang sama maka secara sederhana dapat dituliska sebagai berikut.
Jika $P=x^{n}$ dengan $x=x_{o}\pm\Delta x$, maka $\frac{\Delta P}{P}=n\frac{\Delta x}{x}$.
4. Aturan Perkalian dengan Konstanta
Jika nilai hasil pengukuran yang mengandung ketidak pastian relatif dikalikan dengan sebuah konstanta maka ketidak pastian relatif tidak ikut dikalikan. Tetapi jika hasil pengukurannya mengandung ketidak pastian mutlak maka nilai ketidak pastian harus ikut dikalikan dengan konstanta.
Jika $x=x_{o}\pm\frac{\Delta x}{x_{o}}$, maka $kx=kx_{o}\pm\frac{\Delta x}{x_{o}}$
Jika $x=x_{o}\pm\Delta x$, maka $kx=kx_{o}\pm k\Delta x$
Contoh Soal & Pembahasan
- Pak Arifin mengukur ketebalan uang logam menggunakan mikrometer sekrup dan diperoleh hasil bahwa ketebalan uang logam adalah 1,80 mm. Penulisan hasil pengukuran yang tepat adalah…
.Penyelesaian:
$x_{0}=1,80$ mm dan nilai skala terkecil = 0,01 mm, maka penulisan yang tepat adalah
$\begin{alignedat}{1}x & =x_{0}\pm\frac{1}{2}\mbox{ nst}\\
& =1,80\pm0,005\mbox{ mm}
\end{alignedat}
$
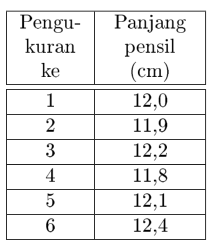
- Suatu pengukuran berulang terhadap panjang pensil diperoleh hasil seperti berikut.

Laporkan hasil pengukuran berulang tersebut lengkap dengan ketidakpastiannya!
Penyelesaian:
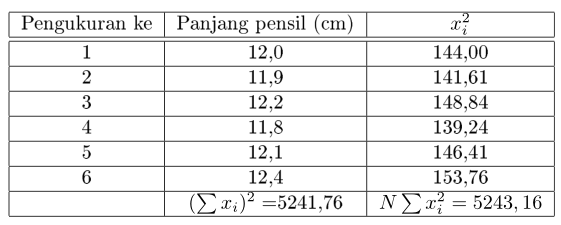
Untuk mempermudah perhitung dapat digunakan tabel seperti berikut.

$\bar{x}=\frac{x_{1}+x_{2}+x_{3}+…..+x_{n}}{N}=\frac{\sum x_{i}}{N}=\frac{72.4}{6}=12,1$ cm
$\Delta x=\frac{1}{N}\sqrt{\frac{N\sum x_{i}^{2}-(\sum x_{i})^{2}}{N-1}}=\frac{1}{6}\sqrt{\frac{5243,16-5241,76}{5}}=0,08$ cm
$\mbox{ketidakpastian relatif}=\frac{0,08}{12,1}\times100\%=0,7\%.$
Karena ketidak pastian relatif dekat dengan 1% maka pelaporan hasil pengukuran hanya berhak dengan 3 angka. Jadi penulisan hasil pengukurrannya adalah $x=12,1\pm0,08$ cm.
- Pengukuran diameter dan tinggi sebuah silinder adalah $\left(80,0\pm0,05\right)$cm
dan $\left(25,0\pm0,05\right)$cm. Nilai prosentase ketidak pastian volume silinder tersebut adalah….
Penyelesaian:
Volume silinder adalah $V=\frac{1}{4}\pi d^{2}t$, sehingga prosentase ketidakpastiannya adalah
$\begin{alignedat}{1}\%\Delta V & =2\%\Delta d+\%\Delta t\\
& =2\times\frac{0,05}{80,0}\times100\%+\frac{0,05}{25,0}\times100\%\\
& =0,125\%+0,2\%\\
& =0,325\%.
\end{alignedat}
$