Modulus Elastisitas merupakan salah satu materi fisika yang cukup menarik untuk dibahas. Kalau kebetulan kamu ingin belajar tentang materi ini lebih dalam, simak penjelasan lengkapnya berikut. Kami juga telah menyediakan soal latihan yang bisa dikerjakan untuk mengasah kemampuanmu.
Lewat pembahasan ini, kamu bisa belajar mengenai Modulus Elastisitas. Kamu akan diajak untuk memahami materi dan tentang metode menyelesaikan soal.
Kamu juga akan memperoleh latihan soal interaktif yang tersedia dalam tiga tingkat kesulitan, yaitu mudah, sedang, dan sukar. Tertarik untuk mempelajarinya?
Sekarang, kamu bisa mulai mempelajari materi lewat uraian berikut. Apabila materi ini berguna, bagikan ke teman-teman kamu supaya mereka juga mendapatkan manfaatnya.
Kamu dapat download modul & kumpulan soal Modulus Elastisitas dalam bentuk pdf pada link dibawah ini:
Definisi
Pasa pengertian modulus elastisitas kita akan memelajari tentang elastisitas yang merupakan kemampuan benda untuk kembali ke keadaan awal segera setelah gaya luar yang diberikan pada benda hilang. Dalam materi rumus modulus elastisitas ini kita akan belajar mengenai 3 Modulus yakni Young, Shear & Bulk
1. Modulus Young
Jika sebuah tongkat sepanjang $L_{i}$ dan luas penampang $A$ ditarik dengan gaya luar sebesar $F$ sehingga panjang tongkat menjadi $L_{f}$ dengan $L_{f}>L_{i}$ maka pada kondisi ini tongkat mengalami tegangan.
Tegangan tarik ($\sigma$) didefinisikan sebagai gaya $(F)$ persatuan luas ($A$) dan regangan tarik ($e$) adalah perbandingan pertambahan panjang ($\Delta L$) dengan panjang mula-mula ($L_{i}$) saat sebuah benda dikenai gaya.
\begin{eqnarray}
\mbox{Tegangan},\sigma & = & \frac{F}{A}\\
\mbox{Regangan }e & = & \frac{\Delta L}{L_{i}}
\end{eqnarray}
Perbandingan antara tegangan dan regangan disebut sebagai Modulus Elastisitas atau Modulus Young (Y). Sehingga dalam hal ini rumus modulus elastisitas atau modulus young adalah sbb:
\begin{eqnarray}
Y & = & \frac{\sigma}{e}\nonumber \\
Y & = & \frac{F\times L}{A\times\Delta L}
\end{eqnarray}
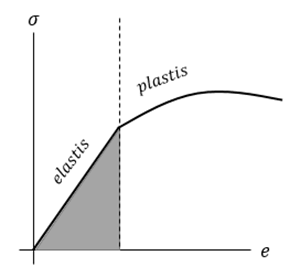
Tidak semua benda dapat kembali ke bentuk semula setelah dikenai gaya. Elastisitas benda hanya berlaku sampai suatu batas yaitu batas elastisitas. Batas elastisitas didefinisikan sebagai tegangan maksimum yang dapat diberikan ke bahan sebelum bahan mengalami deformasi permanen.
Pada suatu titik benda yang diberi gaya dan mengalami deformasi tidak dapat kembali ke bentuk semula. Titik inilah yang disebut batas elastis. Pada benda yang elastis, perbandingan tegangan dengan regangannya adalah konstan.
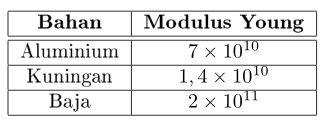
Setiap bahan memiliki nilai Modulus Young berbeda-beda. Tabel 1 menunjukkan beberapa nilai modulus Young dari beberapa bahan. Seperti modulus elastisitas beton bertulang berbeda dengan modulus elastisitas baja untuk lebih jelasnya dapat dilihat pada tabel 1.
2. Modulus Shear
Tipe deformasi yang lain ketika sebuah objek dikenai gaya adalah saat objek dikenai gaya yang sejejar dengan luas penampang benda. Misalkan benda awalnya berbentuk balok kemudian dikenai gaya di salah satu sisinya kemudian balok menjadi berbentuk prisam jajargenjang, pada kondisi ini maka benda mengalami tegangan geser.

Perhatikan gambar di atas! Modulus Shear ($S$) didefinisikan sebagai perbandingan tegangan geser dengan regangan geser. Tegangan geser adalah gaya yang bekerja persatuan luas, dimana gaya bekerja sejajar dengan luas penampangnya. Regangan geser adalah perbandingan pergeseran sisi ($\Delta x$) dengan tinggi objek ($h$)
\begin{eqnarray}
S & = & \frac{F/A}{\Delta x/h}\nonumber \\
S & = & \frac{F\times h}{A\times\Delta x}
\end{eqnarray}
Satuan modulus elastisitas yakni satuan dari Modulus Young dan Modulus Shear adalah sama yaitu $\mbox{N/m}^{2}.$
3. Modulus Bulk
Modulus Bulk adalah nilai yang menggambarkan toleransi sebuah bahan terhadap perubahan volume jika dikenai gaya. Modulus Bulk didefinisikan sebagai perbandingan tegangan volume dengan regangan volume.
Tegangan volume adalah gaya persatuan luas dan regangan volume adalah perbandingan perubahan volume ($\Delta V$) dengan volume mula-mula $(V_{i})$. Secara matematis Modulus Bulk ($B$) dituliskan sebagai berikut.
\begin{eqnarray}
B & = & \frac{\Delta F/A}{\Delta V/V_{i}}\nonumber \\
S & = & \frac{\Delta P\times V_{i}}{\Delta V}
\end{eqnarray}
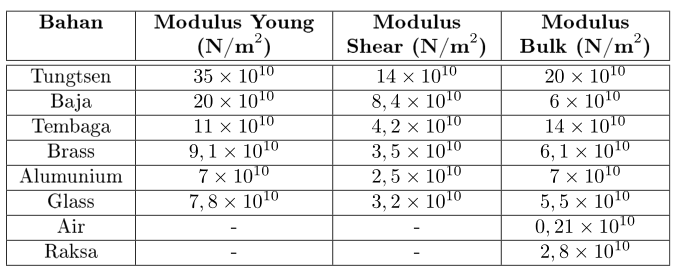
Tabel 1. Nilai Modulus Beberapa Bahan.
Contoh Soal Modulus Elastisitas & Pembahasan
- Kawat Baja sepanjang $4$ meter memiliki luas penampang sebesar $1\times10^{-6}\mbox{m}^{2}$ diberi gaya sebesar 1 N. Hitung pertambahan panjang kawat baja tersebut!
Penyelesaian:
Kita dapat menggunakan persamaan (3) untuk menyelesaikan soal ini.
$\begin{alignedat}{1}Y & =\frac{F\times L}{A\times\Delta L}\\
\Delta L & =\frac{F\times L}{A\times Y}\\
& =\frac{1\times4}{1\times10^{-6}\times20\times10^{10}}\\
& =2\times10^{-5}\mbox{ m}
\end{alignedat}
$
- Kawat tembaga sepanjang $5,5$ meter memiliki luas penampang sebesar $1\times10^{-6}\mbox{m}^{2}$. Berapa gaya yang harus diberikan agar kawat bertambah panjang 1 mm?
Penyelesaian:
Kita dapat menggunakan persamaan (3) untuk menyelesaikan soal ini.
$\begin{alignedat}{1}Y & =\frac{F\times L}{A\times\Delta L}\\
F & =\frac{Y\times A\times\Delta L}{L}\\
& =\frac{11\times10^{10}\times1\times10^{-6}\times1\times10^{-3}}{5,5}\\
& =20\mbox{ N}
\end{alignedat}
$